
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Гамма-функція
Біноміальна теорема визначає біноміальні коефіцієнти через факторіали чисел n і k:
 .
.
По суті, факторіал 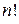 є|з'являється,являється| функцією аргументу n. Проте|однак| це дискретна (гратчаста) функція, визначена тільки|лише| при цілих значеннях аргументу n = 1, 2, ... Тому формула (4.2) придатна тільки|лише| для цілих n.
є|з'являється,являється| функцією аргументу n. Проте|однак| це дискретна (гратчаста) функція, визначена тільки|лише| при цілих значеннях аргументу n = 1, 2, ... Тому формула (4.2) придатна тільки|лише| для цілих n.
Виникає питання: чи існує безперервна функція безперервного аргументу, яка в окремих випадках цілого аргументу n = n дорівнювала|рівнялася| б 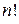 ? На це питання існує позитивна відповідь. Така функція існує і називається вона гамма-функцією (Г-функцією). Ця функція володіє властивістю:
? На це питання існує позитивна відповідь. Така функція існує і називається вона гамма-функцією (Г-функцією). Ця функція володіє властивістю:  . Її графік приведений на мал. 4.3.
. Її графік приведений на мал. 4.3.

Мал. 4.3. Графік гамма-функції
Гамма-функція визначається за допомогою інтеграла Ейлера:
 ,
,
де n > 0.
При£ n £ 0 інтеграл розходиться. У цьому інтервалі за допомогою інтеграла Ейлера гамма-функція не може бути визначена. При n = 1 маємо:
 .
.
Прийнявши в інтегралі Ейлера x = t2, одержимо|отримаємо|
 .
.
Прирівнявши n = 1/2, маємо
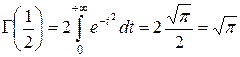 .
.
Застосуємо до інтеграла Ейлера формулу інтегрування по частинах|частках|: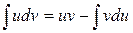 , вважаючи|гадаючи|
, вважаючи|гадаючи| 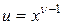 ;
;  ;
;  ;
;  .
.

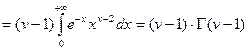 .
.
Це основна формула приведення для Г-функції. З|із| неї виходить, що
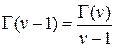 .
.
Застосував цю формулу послідовно k разів, одержимо:
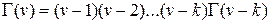 , (n – k > 0).
, (n – k > 0).
У математичних| довідниках значення гамма-функції звичайно даються лише для величин v, лежачих в діапазоні 1 < n < 2. щоб знайти значення Г-функції в іншому діапазоні, потрібно використовувати приведену формулу. Для знаходження Г(n) при n > 2 ми повинні вибирати ціле k > 0 так, щоб|так , щоб,таким образом | виконувалося умови: 1 £ n – k < 2.
Якщо n = n, де n > 0 – ціле число, то
Г (n) = (n – 1)!
Застосувавши формулу приведення для n = n + 1/2 і враховуючи, що, одержимо|отримаємо|
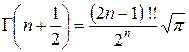 ,
,
де (2n – 1)!! = 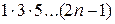 .
.
Дотепер|до цих пір| ми вважали|лічили|, що аргумент n функції Г(n) більше нуля. Довизначимо тепер функцію гамма для негативних|заперечних| значень аргументу. Враховуючи формулу приведення, запишемо:
 .
.
Покладемо  = n*, тоді
= n*, тоді
 .
.
Позначивши в останній формулі n* знову через, одержимо|отримаємо|
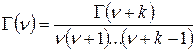 .
.
Якщо n + до > 0 і  . (
. ( = 1, 2, 3...), то права частина|частка| формули має сенс і при n < 0. Останню формулу приймають за визначення гамма-функції при негативних|заперечних| значеннях аргументу n. Очевидно, вона не існують при цілих негативних|заперечних| значеннях n (при таких значеннях n вона звертається|обертається| в нескінченність).
= 1, 2, 3...), то права частина|частка| формули має сенс і при n < 0. Останню формулу приймають за визначення гамма-функції при негативних|заперечних| значеннях аргументу n. Очевидно, вона не існують при цілих негативних|заперечних| значеннях n (при таких значеннях n вона звертається|обертається| в нескінченність).
Тепер ми можемо узагальнити біноміальну теорему на випадок дійсних (і навіть комплексних чисел).
Теорема 4.2. Хай|нехай|  – довільне комплексне число. Тоді для будь-якого комплексного числа, що задовольняє умові, справедливо
– довільне комплексне число. Тоді для будь-якого комплексного числа, що задовольняє умові, справедливо
 (4.3)
(4.3)
де 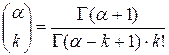 .
.
Приклад|зразок| 4.1. Приведемо приклади|зразки| деяких біноміальних розкладань, одержаних за допомогою формули (4.3):
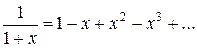

| <== попередня сторінка | | | наступна сторінка ==> |
| Біном Ньютона для дробових і негативних|заперечних| показників | | | Розміщення без повторень |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |