• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розміщення без повторень

Лекція № 5. КОМБІНАТОРИКА

5.1. Вступ|вступ|

У багатьох практичних випадках виникає необхідність підрахувати|підсумувати| кількість можливих комбінацій об'єктів, що задовольняють певним умовам. Такі завдання|задачі| називаються комбінаторними. Розділ математики, який їх вивчає, називається комбінаторикою.

Одними з найбільш важливих|поважних| понять комбінаторики є|з'являються,являються| розміщення і поєднання.

Спосіб розташування в певному порядку|ладі| деякого числа елементів із|із| заданої множини|безлічі|, коли істотна|суттєва| послідовність вибору елементів, називається розміщенням. Якщо ж послідовність вибору елементів неістотна|несуттєва|, то спосіб вибору називається поєднанням.

Приклад|зразок| 5.1. Дано безліч S, що складається з трьох елементів: а, b, с. Необхідно визначити кількість комбінацій по два елементи з|із| представлених|уявлених| трьох.

1. Повторення елементів не допускається:

а) існує 6 розміщень (ab, ас, ba, bc, ca, cb);

б) існує 3 поєднання (ab, bc, ca).

2. Повторення елементів вирішується:

а) існує 9 розміщень (ab, aa, ас, ba, bb, bc, ca, cb, cc);

б) існує 6 поєднань (aa, ab, ас, bb, bc, cc).

Загальне|спільне| число розміщень без повторень з|із| n елементів по елементів позначається|значиться| так: .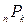

Теорема 5.1.

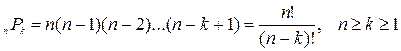. (5.1)

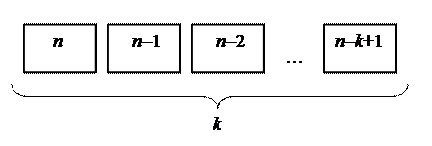
Доказ. Завдання|задача| зводиться до заповнення порожніх|пустих| місць символами елементів (мал. 5.1).

Мал. 5.1

Перше місце можна заповнити n різними способами, оскільки є|наявний| n елементів, і повторення не допускаються. Друге місце n – 1 способом, оскільки один елемент вже задіяний. Третє місце n – 2 способами, оскільки два елементи вже задіяні і т.д. Останнє -те| місце можна заповнити 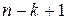різними способами. Загальна|спільна| кількість розміщень буде рівна добичі|добутку| способів заповнення кожного з порожніх|пустих| місць.

Слідство|наслідок|. При n =

Розміщення (при n = ) називається перестановкою.

Приклад|зразок| 5.2. Якщо дано множину|безліч|, що складається з трьох елементів: а, b і с|із|, та кількість розміщень по два елементи рівна, що відповідає результату, приведеному в прикладі|зразку| 5.1.

Читайте також:

1. Вибір кількості та розміщення складської мережі
2. Вибір типу і місця розміщення водозабірних споруд
3. Вибір, розміщення, режими роботи компенсуючих пристроїв.
4. Вивіз капіталу та інвестиції в системі міжнародних економічних відносин. Напрямки та структура вивозу капі­талу. Форми вивозу та розміщення (інвестування) капіталу.
5. Вимоги до розвитку та розміщення об’єктів атомної енергетики
6. Вимоги до розміщення потенційно-небезпечних виробництв
7. Вплив науково-технічного прогресу на розміщення продуктивних сил
8. Вплив розміщення оборотних коштів підприємства на його фінансовий стан.
9. Грошовий потік від розміщення 3-літньої облігаційної позики, тис. грн.
10. Грошовий потік від розміщення 5-літньої облігаційної позики, тис. грн.
11. Демографічні передумови розміщення продуктивних сил.
12. Економічні закони і закономірності розміщення продуктивних сил.

Переглядів: 2411