
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Приклад|зразок| 8.1.
15 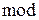 2 =
2 =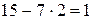 ,
,
26 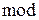 3 =
3 = ,
,
32 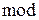 4 =
4 =  .
.
Хай|нехай| є|наявний| генератор псевдовипадкових чисел, що працює по певному алгоритму. Часто використовується наступний|слідуючий| алгоритм:
 (8.1)
(8.1)
де  – попереднє псевдовипадкове число,
– попереднє псевдовипадкове число,  – подальше|наступне| псевдовипадкове число, а коефіцієнти а, b, с|із| постійні і добре відомі. Звичайно c=
– подальше|наступне| псевдовипадкове число, а коефіцієнти а, b, с|із| постійні і добре відомі. Звичайно c= , де
, де 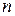 – розрядність процесора,
– розрядність процесора,  , а b – непарне. В цьому випадку послідовність псевдовипадкових чисел має період с.
, а b – непарне. В цьому випадку послідовність псевдовипадкових чисел має період с.
Приклад|зразок| 8.2.У табл. 8.1 приведені результати розрахунків по формулі (8.1) для різних ключів|джерел| шифру  і коефіцієнтів: a=81, b=9, c=65536.
і коефіцієнтів: a=81, b=9, c=65536.
Таблиця 8.1

| 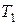
| 
| 
| 
| 
| 
| 
| 
| 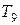
| 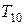
|
Процес шифрування визначається таким чином. Шифроване повідомлення|сполучення| представляється у вигляді послідовності слів, кожне довжини, які складаються по модулю два із|із| словами послідовності, тобто|цебто|
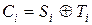 .
.
Послідовність  називається гаммою шифру. Процес розшифровки полягає в тому, щоб ще раз скласти шифровану послідовність з|із| тією ж самою гаммою шифру:
називається гаммою шифру. Процес розшифровки полягає в тому, щоб ще раз скласти шифровану послідовність з|із| тією ж самою гаммою шифру:
 .
.
Ключем|джерелом| шифру є|з'являється,являється| початкове значення, яке є|з'являється,являється| секретним і повинно бути відомо тільки|лише| відправнику і одержувачу шифрованого повідомлення|сполучення|. Шифри, в яких для зашифровуваної і розшифровки використовується один і той же ключ|джерело|, називаються симетричними.
Описаний метод шифрування володіє істотним|суттєвим| недоліком|нестачею|. Якщо відома хоч би частина|частка| початкового|вихідного| повідомлення|сполучення|, то все повідомлення|сполучення| може бути легко дешифровано. Дійсно, хай|нехай| відоме одне початкове|вихідне| слово 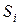 . Тоді
. Тоді
 ,
,
і далі вся права частина|частка| гамми шифру визначається по вказаній формулі генератора псевдовипадкових чисел.
Для підвищення криптостойкости симетричних шифрів застосовуються різні прийоми.
· Обчислення|підрахунок| гамми шифру по ключу|джерелу| складнішим (або секретним) способом.
· Застосування|вживання| замість  складнішої (але|та| оборотної операції) для обчислення|підрахунку| шифровки|шифрування|.
складнішої (але|та| оборотної операції) для обчислення|підрахунку| шифровки|шифрування|.
· Попереднє перемішування бітів початкового|вихідного| повідомлення|сполучення| по фіксованому алгоритму.
В даний час|нині| широкого поширення набули шифри з|із| відкритим|відчиненим| ключем|джерелом|. Ці шифри не є|з'являються,являються| симетричними – для зашифровуваної і розшифровки використовуються різні ключі|джерела|. При цьому ключ|джерело|, використовуваний для зашифровуваної, є|з'являється,являється| відкритим|відчиненим| (не секретним) і може бути повідомлений всім охочим відправити шифроване повідомлення|сполучення|. А ключ|джерело|, використовуваний для розшифровки, є|з'являється,являється| закритим|зачиненим| і зберігається у секреті одержувачем шифрованих повідомлень|сполучень|. Навіть знання всього зашифрованого повідомлення|сполучення| і відкритого|відчиненого| ключа|джерела|, за допомогою якого його було зашифровано, не дозволяє дешифрувати повідомлення|сполучення| без знання закритого|зачиненого| ключа|джерела|.
Для опису методу шифрування з|із| відкритим|відчиненим| ключем|джерелом| потрібні деякі факти з|із| теорії чисел, викладені (без доказу) в наступному|такому| розділі.
Читайте також:
| <== попередня сторінка | | | наступна сторінка ==> |
| Лекція № 8. ШИФРУВАННЯ | | | Модулярна арифметика |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |