• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Приклад|зразок| 8.4.

Приклад|зразок| 8.3.

,

,

.

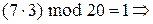
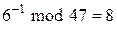Функція: – називається функцією Ейлера. Якщо 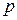– просте число, то , і взагалі .

Можна показати, що

,

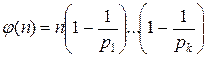де – всі прості дільники n.

,

, .

,

, .

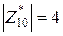Теорема 8.1. (Ейлера). Якщо , то .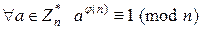

Приклад|зразок| 8.5.Хай|нехай| n=10. Тоді і .

,

,

,

.

З|із| теореми Ейлера безпосередньо виводиться

Теорема 8.2. (мала теорема Ферма). Якщо , то .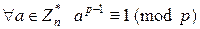

Має місце наступне|таке| твердження|затвердження|

Теорема 8.3. Якщо числа попарно взаємно прості, число 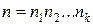– їх добич|добуток|, x і а – цілі числа, то .

Останнє твердження|затвердження| є|з'являється,являється| слідством|наслідком| теореми, яка відома як «китайська теорема про залишки».

Приклад|зразок| 8.6.Хай|нехай| n=10=; x=81; a=61. Тоді

, , ,

, , .

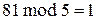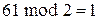8.3. Шифрування з|із| відкритим|відчиненим| ключем|джерелом|

Шифрування з|із| відкритим|відчиненим| ключем|джерелом| проводиться|виробляється,справляється| таким чином.

1. Одержувачем повідомлень|сполучень| проводиться|виробляється,справляється| генерація відкритого|відчиненого| ключа|джерела| (пара чисел n і e) і закритого|зачиненого| ключа|джерела| (число d). Для цього:

· вибираються два прості числа p і q;

· визначається перша частина|частка| відкритого|відчиненого| ключа|джерела| n=pq;

· визначається друга частина|частка| відкритого|відчиненого| ключа|джерела| – вибирається невелике непарне число e, взаємно простої з|із| числом (відмітимо|помітимо|, що );

· визначається закритий|зачинений| ключ|джерело|: .

Після чого відкритий|відчинений| ключ|джерело| (числа n і e) повідомляється всім відправникам повідомлень|сполучень|.

2. Відправник шифрує повідомлення|сполучення| (розбиваючи його, якщо потрібно, на слова 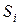завдовжки менш 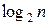розрядів):

,

і відправляє|відряджає| одержувачу.

3. Одержувач розшифровує повідомлення|сполучення| за допомогою закритого|зачиненого| ключа|джерела| d:

.

Теорема 8.4. Шифрування з|із| відкритим|відчиненим| ключем|джерелом| коректно, тобто|цебто| в прийнятих позначеннях .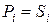

Доказ. Очевидно, що . Покажемо, що . Дійсно числа d і e взаємно зворотні по модулю, тобто|цебто|

при деякому. Якщо 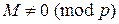, то по малій теоремі Ферма маємо:

.

Якщо , то порівняння , очевидно, виконується. Таким чином

.

Абсолютно|цілком| аналогічно маємо

.

І по слідству|наслідку| до китайської теореми про залишки

.

Оскільки і , укладаємо|ув'язнюємо,замикаємо,поміщаємо|, що .

Приклад|зразок| 8.7.Генерація ключів|джерел|:

1. p=3, q=11;

2. n=;

3. , e=7;

4. d=, ().

Хай|нехай| =3, =1, =2 (). Тоді код визначається таким чином:

;

;

.

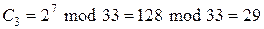При розшифровці маємо:

,

,

.

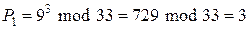Шифри з|із| відкритим|відчиненим| ключем|джерелом| порівняно прості в реалізації, дуже практичні (оскільки немає необхідності пересилати по каналах зв'язку закритий|зачинений| ключ|джерело| і можна безпечно зберігати його в одному місці) і в той же час володіють високою криптостійкістю.

Здається|видається|, що дешифрувати повідомлення|сполучення| нескладно: досить розкласти відкрито|відчинений| опубліковане число n на множники, відновивши числа p і q, і далі можна легко обчислити|обчисляти,вичислити| секретний ключ|джерело| d.

Проте|однак| справа|річ| полягає в наступному|слідуючому|. В даний час|нині| відомі ефективні алгоритми визначення простоти чисел, які дозволяють за декілька хвилин підібрати|добрати| пару дуже великих простих чисел (по 100 і більше цифр в десятковому записі). В той же час невідомі ефективні алгоритми розкладання дуже великих чисел на множники. Розкладання на множники числа в 200 і більше цифр зажадало б сотень років роботи найкращого суперкомп'ютера. При практичному застосуванні|вживанні| шифрів з|із| відкритим|відчиненим| ключем|джерелом| використовують дійсно великі прості числа (не менше 100 цифр в десятковому записі, а звичайно – значно більше|значно більший|). В результаті розкрити|розітнути| цей шифр виявляється|опиняється| неможливо, якщо не існує ефективних алгоритмів розкладання на множники.

Втім, можливість|спроможність| відкриття|відчинення| таких алгоритмів існує, хоча цей факт і не доведений строго|суворо|.

Читайте також:

1. Приклад|зразок| 8.1.

Переглядів: 569