
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Основні визначення
Лекція № 12. НЕОРІЄНТОВАНІ ГРАФИ
Граф 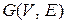 – це сукупність двох множин|безлічі|: вершин
– це сукупність двох множин|безлічі|: вершин 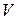 і ребер
і ребер  , між якими визначено відношення|ставлення| інцидентності.
, між якими визначено відношення|ставлення| інцидентності.
Кожне ребро e з|із| E інцидентно рівно двом вершинам 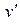 і
і 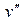 , які воно сполучає|поєднує,з'єднує|. При цьому вершина
, які воно сполучає|поєднує,з'єднує|. При цьому вершина 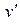 і ребро e називаються інцидентними один одному, а вершини
і ребро e називаються інцидентними один одному, а вершини 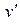 і
і 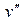 називаються суміжними.
називаються суміжними.
Прийнято позначення n для числа вершин графа (потужність множини|безлічі| 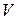 ):
):  і m для числа його ребер:
і m для числа його ребер: 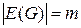 . Говорять, що граф G є (n, m) граф, де n – порядок|лад| графа, m – розмір графа.
. Говорять, що граф G є (n, m) граф, де n – порядок|лад| графа, m – розмір графа.
Якщо всі ребра 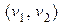 графа неорієнтовані, тобто пари вершин, які визначають елементи множини E, неврегульовані, то такий граф називається неорієнтованим графом, або неографом|. На мал. 12.1 показаний приклад|зразок| неографа|. Цей граф має п'ять вершин і шість ребер.
графа неорієнтовані, тобто пари вершин, які визначають елементи множини E, неврегульовані, то такий граф називається неорієнтованим графом, або неографом|. На мал. 12.1 показаний приклад|зразок| неографа|. Цей граф має п'ять вершин і шість ребер.

Мал. 12.1
Маршрут – послідовність ребер, в якій кожні два сусідні ребра мають загальну|спільну| вершину. Граф зв'язний, якщо будь-які дві вершини сполучені|з'єднані| хоч би одним маршрутом. Число ребер маршруту визначає його довжину.
Ребра, інцидентні одній парі вершин, називаються паралельними або кратними. Граф з|із| кратними ребрами називається мультиграфом.
Ребро 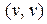 називається петлею (кінцеві вершини співпадають|збігаються|). Граф, що містить|утримує| петлі і кратні ребра, називається псевдографом. На мал. 12.2 показаний псевдограф.
називається петлею (кінцеві вершини співпадають|збігаються|). Граф, що містить|утримує| петлі і кратні ребра, називається псевдографом. На мал. 12.2 показаний псевдограф.

Мал. 12.2
Ступінь|міра| deg(v) вершини – це число ребер, інцидентних v. У неографі| сума ступенів|мір| всіх вершин рівна подвоєному числу ребер (лема про рукостискання):
 . (12.1)
. (12.1)
Петля дає внесок|вклад|, рівний 2, в ступінь|міру| вершини.
Статечна|поважна| послідовність – послідовність ступенів|мір| всіх вершин графа, записана в певному порядку|ладі| (за збільшенням або убуванню).
Приклад|зразок| 12.1. Статечна|поважна| послідовність неографа|, зображеного|змальованого| на мал. 12.1, записана за збільшенням, виглядає так:
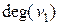 =1,
=1, 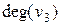 =2,
=2, 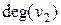 =3,
=3,  =3,
=3, 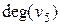 =3.
=3.
Сума ступенів|мір| всіх вершин графа рівна:
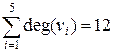 .
.
Цей результат не суперечить|перечить| лемі про рукостискання, оскільки граф має шість ребер (m = 6).
Матриця суміжності графа – квадратна матриця A порядку|ладу| n, де елемент  рівний числу ребер, що сполучають|поєднують,з'єднують| вершини i і j.
рівний числу ребер, що сполучають|поєднують,з'єднують| вершини i і j.
Приклад|зразок| 12.2. Граф, показаний на мал. 12.1, має наступну|таку| матрицю суміжності
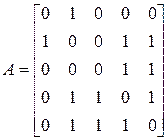 .
.
Матриця інцидентності I – ще один спосіб опису графа. Число рядків цієї матриці рівне числу вершин, число стовпців – числу ребер;  =1, якщо вершина v інцидентна ребру e; інакше
=1, якщо вершина v інцидентна ребру e; інакше  =0. У кожному стовпці матриці інцидентності простого графа (без петель і без кратних ребер) міститься|утримується| по дві одиниці. Число одиниць в рядку рівне ступеню|мірі| відповідної вершини.
=0. У кожному стовпці матриці інцидентності простого графа (без петель і без кратних ребер) міститься|утримується| по дві одиниці. Число одиниць в рядку рівне ступеню|мірі| відповідної вершини.
Приклад|зразок| 12.3. Граф, показаний на мал. 12.1, має наступну|таку| матрицю інцидентності
 .
.
Граф  називається підграфом графа
називається підграфом графа 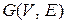 , якщо
, якщо  і
і 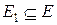 . Якщо
. Якщо 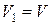 , то підграф називається остовним|.
, то підграф називається остовним|.
Компоненту зв'язності графа – максимальний по включенню|приєднанню| вершин і ребер зв'язкової підграф.
Ранг графа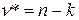 , де k – число компонент зв'язності.
, де k – число компонент зв'язності.
Дерево – зв'язковий граф, що містить|утримує| n – 1 ребро.
Приклад|зразок| 12.4. На мал. 12.3 показане дерево, яке одночасно є|з'являється,являється| остовним| підграфом графа, показаного на мал. 12.1.

Мал. 12.3
Читайте також:
- I визначення впливу окремих факторів
- II. Визначення мети запровадження конкретної ВЕЗ з урахуванням її виду.
- II. Мотивація навчальної діяльності. Визначення теми і мети уроку
- II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
- Ocнoвнi визначення здоров'я
- Адвокатура в Україні: основні завдання і функції
- Алгебраїчний спосіб визначення точки беззбитковості
- Амортизація основних засобів, основні методи амортизації
- Аналіз службового призначення деталей та конструктивних елементів обладнання харчових виробництві, визначення технічних вимог і норм точності при їх виготовленні
- Аналіз стратегічних альтернатив та визначення оптимальної стратегії формування фінансових ресурсів
- Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
- Артеріальний пульс, основні параметри
| <== попередня сторінка | | | наступна сторінка ==> |
| Приклад|зразок| 8.4. | | | Ребровий граф |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |