• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розв’язування ЗЛП графічним методом

Розглянемо найпростіший випадок n=2.

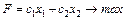
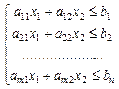
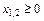
Така задача називається плоскою. Кожна нерівність системи обмежень визначає частину площини, що лежить вище (нижче) відповідної прямої. Уся система обмежень визначає на площині х₁, х₂ багатокутник, що називається припустимою областю (припустимою множиною) задачі.

Кожна точка Р(х₁, х₂ ) усередині цієї множини і на її межі визначає припустимий план задачі. Необхідно з усіх припустимих планів задачі знайти найкращий (оптимальний).

Вектор 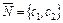є градієнтом функції F і перпендикулярний до лінії рівня F=const.

Проведемо лінію рівня F=0 - пряма l: с₁х₁ + с₂х₂ = 0 проходить через початок координат. Побудуємо 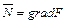у точці О(0;0) і виконаємо паралельне перенесення прямої l у напрямку 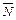. У процесі перенесення пряма проходить через різні точки припустимої множини. Точка, у якій відбувається останнє торкання цією прямою області (точка «прощання») і визначає оптимальний план задачі. Якщо «прощання» відбувається по стороні багатокутника, кожна її точка дає оптимальний план; задача має безліч рішень. Якщо такої точки не існує, задача не має рішень.

Приклад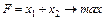

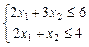
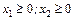
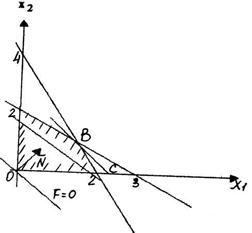
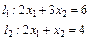А (0;2); В (1,5;1); С (2;0)

Припустима множина: чотирикутник ОАВС. Точка «прощання» В (1,5;1).

Оптимальний план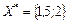

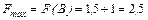
2. Розглянемо задачу лінійного програмування в канонічній формі

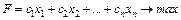(2.1)

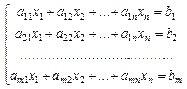(2.2)

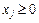; j= 1,... n (2.3)

Введемо в розгляд матриці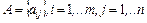

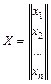
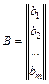
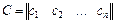
Задача набуде наступного вигляду:

F = С • X"max (2.4)

А• Х=У (2.5)

X ≥ 0 (2.6)

Система обмежень (2.2) і (2.3) (або (2.5) і (2.6)) задає припустиму множину - багатогранник (симплекс) у n-мірному просторі.

Точка максимуму знаходиться в одній з вершин багатогранника.

Ціль симплекса-методу: за найменше число кроків знайти цю вершину.

Читайте також:

1. VII. Нахождение общего решения методом характеристик
2. АВТОМАТИЗАЦІЯ РОЗВ’ЯЗУВАННЯ КОМПЛЕКСУ ЗАДАЧ З ОБЛІКУ ОСНОВНИХ ЗАСОБІВ ТА НЕМАТЕРІАЛЬНИХ АКТИВІВ
3. Алгоритм розв’язування задачі
4. Алгоритм розв’язування задачі
5. Алгоритм розв’язування задачі
6. Алгоритм розв’язування задачі
7. Алгоритм розв’язування задачі
8. Алгоритм розв’язування задачі
9. Алгоритм розв’язування задачі оптимізації в Excel
10. Аналіз перед розв’язуванням задачі
11. Аналіз перед розв’язуванням задачі
12. Аналіз причин виникнення проблеми та обґрунтування її розв’язання програмним методом

Переглядів: 456