Особливості захисту електронних грошей

У багатьох країнах сплачують за придбані речі при допомозі електронних карток, які дозволяють також замовляти авіаквитки через Інтернет, купувати найрізноманітніші товари в Інтернет-магазинах. Відомості про покупки накопичуються в магазинах і банках. Тому з’явилася нова проблема, іноді названа як „проблема Великого Брата”.

Суть проблеми полягає в тому, що зникає анонімність процесу купівлі, тобто інформація про покупки будь-якої особи може стати відомою третім особам і використовуватися проти неї. Наприклад, відомості щодо придбання квитка на потяг чи літак можуть становити інтерес для злочинців тощо. Тому виникла ідея розробити такі схеми електронних платежів, які б зберігали анонімність покупця тією самою мірою, що й при розрахунку готівкою. Такі протоколи називаються електронними, або цифровими грошима (digital cache), що підкреслює їхню головну властивість – забезпечувати такий самий ступінь анонімності, як і звичайні гроші. Деякі схеми вже використовуються в реальному житті.

Нехай є така задача. Є три учасники: банк, покупець і магазин. Покупець і магазин мають відповідні рахунки в банку, і покупець хоче придбати товар в магазині. Купівля здійснюється у вигляді триступінчастого процесу:

1) покупець знімає потрібну суму зі свого рахунку в банку;

2) покупець „пересилає” гроші до магазину;

3) магазин повідомляє про це банк, відповідна сума грошей зараховується на рахунок магазину, а покупець забирає товар (чи останній йому доставляється).

Наша мета – обрати таку схему, щоб вона була надійна; щоб банк не знав, хто саме купив товар, тобто було збережено анонімність звичайних грошей.

В одному з варіантів такої схеми можна використати певну односпрямовану функцію F(х). Функція F не є секретна і відома всім (покупцеві, банку і магазину). Банкнота тепер визначається як пара чисел (х, 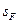), де

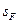
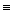[F(х)] mod n,

тобто підписується не х, а значення F(х).

Покупець генерує х (нікому його не показуючи), обчислює F(х), підписує в банку за допомогою „сліпого” підпису число F(х) і формує банкноту (х, ).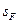

Ця банкнота має всі позитивні властивості, як і в другій схемі, але підробити таку банкноту неможливо, так само як неможливо обчислити обернену функцію. Для перевірки підпису (тобто справжності банкноти) потрібно обчислити F(х) і переконатися, що

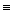(mod n) F(х).

Зауважимо, що при виборі односпрямованих функції слід виявляти обережність. Наприклад, функція F(x) 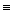а mod n не підходить для певного протоколу. На практиці в якості F(x) завжди використовуються криптографічні геш-функції. Вся решта дій магазину та банку залишається такими самими, як і в раніш описаних схемах.

Існує ще один, більш простий, спосіб боротьби з мультиплікативною властивістю системи RSA – внесення надлишковості в повідомлення. Припустімо, що довжина модуля n – 1024 біти. Такою самою може бути й довжина числа х. Будемо записувати (випадково обираючи) номер банкноти лише в молодші 512 біт х, а в старші 512 біт х запишемо певне фіксоване число.

Це фіксоване число може містити корисну інформацію, таку, приміром, як номінал банкноти та назва банку. Тепер банк при пред’явленні йому банкноти неодмінно перевірятиме наявність фіксованого заголовка в параметрі х і відкидати банкноту в разі його відсутності. Ймовірність того, що при множенні двох чисел за модулем n результат буде збіжним з ними в 512-ти бітах, є неймовірно мала. Тому отримати фальшиву банкноту за формулою не вдасться.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Електронний цифровий підпис. Класифікація атак на ЕЦП	\|	Проблеми безпеки та захист стаціонарного телефонного і стільникового зв’язку

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.016 сек.