• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Електростатичному полі

Провідник в зовнішньому

Розділ 3. Провідник в зовнішньому електростатичному полі

5.1. Рівновага зарядів в провіднику

Носії заряду в провіднику здатні переміщуватись під дією досить малої сили і тому для рівноваги зарядів на провіднику повинні виконуватися умови:

1) напруженість поля всюди всередині провідника дорівнює нулю

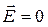. (5.1)

Це означає, в свою чергу означає, що потенціал повинен бути постійним , φ=const.

2) напруженість поля на поверхні провідника в кожній точці направлена по нормалі до поверхні

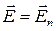. (5.2)

Тому у випадку рівноваги зарядів поверхня провідника буде еквіпотенціальною.

Якщо якомусь тілу надати деякий заряд Q, то він розподілиться так, щоб виконувались умови рівноваги..

Уявимо довільну замкнену поверхню, яка повністю знаходиться в межах тіла. При рівновазі зарядів поле в кожній точці всередині провідника відсутнє, тому потік вектора діелектричного зміщення дорівнює нулю.

.

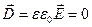Тоді згідно теореми Гауса сумарний заряд всередині поверхні також дорівнює нулю (для поверхні будь-яких розмірів, що проведена довільним чином всередині провідника). Звідси, при рівновазі в жодному місці всередині провідника не може бути залишкових зарядів: всі вони розподілені по поверхні з деякою поверхневою густиною σ.

Оскільки залишкових зарядів немає, видалення речовини з деякого об’єму, який знаходиться всередині провідника не відобразиться на рівноважному розташуванні зарядів. Таким чином, залишковий заряд розподілений на полому провіднику так само, як і на суцільному провіднику (з серцевиною), тобто по його зовнішній поверхні. На поверхні цієї пустоти в стані рівноваги залишкові заряди розташовуватися не можуть. Це витікає і з того, що однойменні елементарні заряди, які утворюють загальний заряд взаємо відштовхуються і прагнуть розташуватися на найбільшій відстані один від одного.

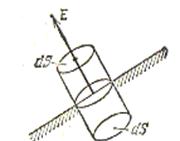Уявимо циліндричну поверхню, утворену нормалями до провідника, з основами dS, одна з яких розташована всередині, а інша – ззовні провідника. Потік вектора електричного зміщення через внутрішню поверхню дорівнює нулю, так як всередині провідника 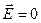, а тому .

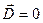Рис. 5.1

Ззовні провідника і в безпосередній близькості до нього напруженість направлена по нормалі до поверхні провідника. Тому для бічної поверхні циліндра, яка знаходиться зовні циліндра D_n=0, а для внутрішньої основи D=D_n, тобто зовнішня основа розташована дуже близько до основи провідника. Відповідно, потік електричного зміщення чисельно дорівнює добутку DdS, де D – величина зміщення в безпосередній близькості до поверхні провідника.

Всередині циліндра знаходиться сторонній заряд

.

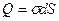Якщо використаємо теорему Гауса, то отримаємо:

DdS= σdS,

D= σ.

Звідси слідує, що напруженість поля поблизу поверхні провідника чисельно дорівнює

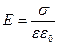, (5.3)

де ε – діелектрична проникливість середовища, яке охоплює даний провідник.

Розглянемо поле, створене зарядженим провідником неправильної форми (рис. 5.2). На великих відстанях від провідника еквіпотенціальні поверхні будуть мати характерні для точкового заряду форму. По мірі наближення до провідника вони стають все більше подібні до поверхні даного провідника.

Поблизу виступів еквіпотенціальні поверхні будуть розташовані густіше, оскільки напруженість поля тут більша.

Тоді густина заряду на виступах досить велика. До такого висновку можна прийти, якщо врахувати, що через взаємне відштовхування зарядів прагнуть розташуватися якомога далі один від одного. Поблизу впадин в провіднику еквіпотенціальні поверхні розташовані рідше, отже напруженість поля і поверхнева густина зряду в цих місцях буде меншою.

Рис. 5.2 Рис. 5.3

Взагалі, густина заряду при даному значенні потенціалу визначається кривизною поверхні і вона збільшується зі збільшенням позитивної кривизни (випуклості) і зменшується з збільшенням негативної кривизни (вгнутості).

Особливо великою буває густина зарядів на вістрі і тому напруженість поля поблизу вістря може бути досить великою, так що на вістрях виникає іонізація молекул газу, який охоплює провідник. Іони іншого знаку, ніж заряд Q притягуються до провідника і нейтралізують його заряд, а іони знаку Q починають рухатися від провідника, захоплюючи нейтральні молекули газу. Виникає рух, який називають „електронним вітром”. Заряд зменшується, стікає з вістря і переноситися „вітром”. Це явище називається витіканням заряду з вістря.

5.2. Провідник в зовнішньому електричному полі

Властивості тіл і їх розміщення в зовнішньому електричному полі визначаються їх будовою.

До складу атомів входять заряджені частинки – електрони і протони. В нормальному стані атом електро-нейтральний (число протонів в ядрі дорівнює числу електронів, які рухаються навколо нього). Електрони утримуються біля ядра силами електричного притягання до ядра, але у металах електрони можуть бути видалені за межі „свого” атома і вільно переміщуватися до тих пір, поки не захопляться іншими атомами.

Електрони, що втратили зв’язок з „своїм” атомом називаються вільними. Їх рух хаотичний і залежить від температури зовнішнього середовища. В металічних провідниках концентрація вільних електронів сягає 10²⁸ м^-3. Такий рух електронів аналогічний до теплового руху вільних газів і тому сукупність вільних електронів називається електронним газом..

Якщо металічний провідник розміщений в електричному полі, то на хаотичний рух електронів накладається впорядкований рух в тому напрямі, який протилежний напруженості поля. Такий рух називається дрейфом..

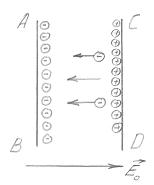Дрейф буде відбуватися в бік поверхні АВ (рис. 5.4), внаслідок чого на CD буде виникати надлишковий позитивний заряд. Явище перерозподілу заряду внаслідок дії зовнішнього електричного поля називається електростатичною індукцією, заряди, що виникають на поверхні провідника називаються наведеними, або індукованими.

Заряди будуть перерозподілятися до тих пір, поки Е₀ не буде дорівнювати протилежно направленій напруженості Е індукованих зарядів.

.

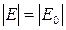Рис.5.4

Напруженість результуючого поля буде дорівнювати нулю і впорядкований рух зарядів припинитися – наступить рівновага.

Якщо на провіднику заряди в рівновазі, то потенціал поля не змінюється. Отже, у випадку рівноваги, поверхня провідника еквіпотенціальна.

5.3. Електроємність. Конденсатори та їх ємність

Експериментально було встановлено, що коли форма і розміри провідника і середовище не змінюються, то при збільшенні заряду пропорційно йому збільшується і потенціал провідника.

,

,

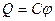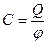де C – електроємність провідника.

Електроємністю провідника або системи провідників називають фізичну величину, яка характеризує здатність провідника накопичувати електричні заряди. В загальному випадку електроємність залежить від середовища і розміщення навколишніх тіл, але не залежить від наданого провіднику заряду і потенціалу.

.

1 Ф – ємність провідника, який змінює потенціал на 1В при зміні заряду на 1Кл.

Ємність провідника, що має форму сфери можна визначити з формули:

,

.

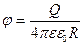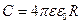Як було сказано, в загальному випадку ємність залежить від середовища, в якому розміщений провідник. Систему провідників, ємність якої не залежить від розміщення навколишніх тіл називають конденсатором – система з двох провідників (обкладок), відокремлених діелектриком, товщина якого мала порівняно з розмірами обкладок. Обкладки конденсатора розташовані так, щоб поле, створене зарядами, було зосереджене в просторі між обкладками.

Ємність конденсатора визначається його геометрією і діелектричними властивостями середовища, яке заповнює простір між обкладками.

В процесі заряджання на обкладках з’являється заряд, однаковий за розміром і протилежний за знаком. Потенціал поля між обкладками змінюється пропорційно заряду обкладок конденсатора.

За формою розрізняють:

1) 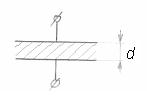плоский конденсатор

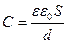, (5.4)

де d – відстань між обкладками, S – площа кожної з обкладок конденсатора.

Рис. 5.5

2) циліндричний конденсатор

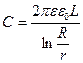, (5.5)

де R, r – радіуси коаксіальних циліндрів, L – довжина твірних.

Рис.5.6

3) сферичний конденсатор

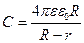, (5.6)

де R, r – радіуси сфер.

Рис.5.7

Якщо конденсатор має декілька діелектриків, то його ємність визначають за формулою:

.

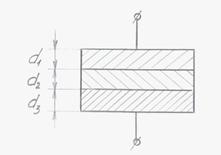
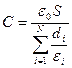Рис.5.8

5.4. З’єднання конденсаторів

Розрізняють паралельне і послідовне з’єднання.

При паралельному з’єднанні конденсаторів вони з’єднуються однойменно зарядженими обкладками. Тоді загальний заряд батареї конденсаторів

Q_заг= Q₁+Q₂+Q₃,

Q₁=U_ABC₁,

Q₂=U_ABC₂ ,

Q₃=U_ABC₃..

Тоді Q_заг=U_AB (C₁ + C₂ + C₃)

Ємність такої батареї

.

Рис.5.9

При паралельному з’єднанні конденсаторів ємність батареї дорівнює сумі ввімкнених ємностей:

.

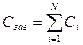При послідовному з’єднанні конденсаторів вони з’єднуються різнойменно зарядженими обкладками.

Загальний заряд батареї: Q_заг= Q₁=Q₂=Q₃.

Напруга між точками А і В:

U_заг= U₁+U₂+U₃.

Рис.5.10

Тобто маємо

.

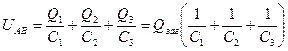При послідовному з’єднанні ємність батареї визначається за формулою:

;

.

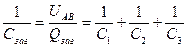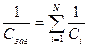Лекція 6

Читайте також:

1. Діелектрики в електростатичному полі.
2. Провідник в електростатичному полі.

Переглядів: 1112