• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розділ 4. Енергія електростатичного поля

§6. Енергія електростатичного поля

6.1. Енергія точкових зарядів

Розглянемо систему з двох точкових зарядів. Знайдемо алгебраїчну суму елементарних робіт сил F₁ i F₂ , з якими взаємодіють заряди. Нехай в системі відліку К за час ∆t заряди здійснили переміщення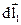і 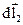, тоді робота цих сил чисельно дорівнює

.

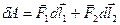Враховуючи те, що сила 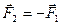згідно з третім законом Ньютона, вираз для роботи можемо переписати у вигляді:

.

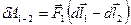Величина в дужках – переміщення заряду 1 відносно заряду 2 в системі К’, яка жорстко зв’язана з зарядом 2 і переміщується з ним поступально по відношенню до даної системи К.

Переміщення 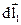заряду 1 в системі К може бути представлене як переміщення 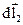системи К’.

Тоді

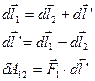
Рис.6.1

З даного виразу бачимо, що сума елементарних робіт в довільній системі відліку К завжди дорівнює елементарній роботі, яку здійснює сила, яка дії на один заряд в системі відліку, де інший заряд знаходиться в стані спокою. Тобто, робота δА ₁₂ не залежить від вибору К-ої системи відліку.

Сила F₁, яка діє на заряд 1 з боку заряду 2 є консервативною і тому робота даної сили по переміщенню на dl₁ може бути представлена як зменшення потенціальної енергії заряду 1 в полі заряду 2, або як зменшення потенціальної енергії взаємодії розглядуваної пари зарядів. Тобто, 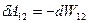. Потенціальна енергія W₁₂ залежить лише від відстані між зарядами.

Перейдемо до системи з трьох зарядів. Роботу, яку здійснюють всі сили взаємодії при переміщенні всіх зарядів можна представити як суму елементарних робіт всіх трьох пар взаємодій.

.

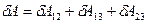Але для кожної пари взаємодій . І тому елементарна робота δА буде визначатися як:

,

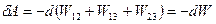де W – повна енергія взаємодії системи зарядів. Кожен доданок залежить від відстані між відповідними зарядами і тому потенціальна енергія взаємодії є функцією конфігурації системи зарядів.

Подібні міркування характерні для системи з будь-яким числом зарядів.

Отже кожній конфігурації довільної системи зарядів має своє значення енергії і робота всіх сил взаємодії при зміні конфігурації буде чисельно дорівнювати зменшенню потенціальної енергії.

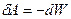. (6.1)

Знайдемо вираз для потенціальної енергії W. Для цього розглянемо систему з трьох точкових зарядів.

.

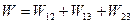Перетворимо цю суму наступним чином: представимо кожний доданок W_ik у вигляді:

(оскільки W_ik=W_ki).

Тоді повна енергія взаємодії перепишеться у вигляді:

.

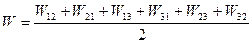Згрупуємо члени з однаковими першими індексами:

.

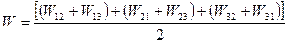Кожна сума в круглих дужках – це енергія W_i взаємодії і-го заряду з двома іншими зарядами. Тому останній вираз можемо записати як суму

.

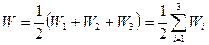Узагальнення на систему із довільного числа зарядів очевидне, бо ясно, що при проведенні розрахунків і міркувань вираз не залежить від числа зарядів. Тому енергія взаємодії системи зарядів в загальному випадку:

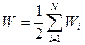. (6.2)

Враховуючи, що з означення потенціалу потенціальна енергія чисельно дорівнює добутку заряду на потенціал поля, в якому він знаходиться

,

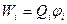де Q_i – і-ий заряд системи, φ_і – потенціал, створений в місці знаходження і-го заряду всіма іншими зарядами системи. Підставимо цей вираз в формулу (6.2) і отримаємо кінцевий вираз для енергії взаємодії системи точкових зарядів.

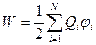. (6.3)

Якщо заряди розподілені неперервно, то розкладаючи систему зарядів на сукупність елементарних зарядів і переходячи від сумування до інтегрування у (6.3) отримаємо, що

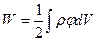, (6.4)

де φ – потенціал, створений всіма зарядами системи в елементі об’ємом dV. Аналогічний вираз можна записати при розподілі зарядів по поверхні:

.

Можна помилково вважати, що рівняння (6.4) – це лише видозмінений вираз (6.3), який відповідає заміні представлення про точкові заряди представленням про неперервний розподіл зарядів. Насправді, ці вирази відрізняються за змістом. Виникнення розбіжності полягає в різному змісті потенціалу φ.

Нехай, система складається з двох кульок, які мають заряди Q₁ i Q₂. Відстань між кульками набагато більша, ніж розміри самих кульок, тому заряди Q₁ i Q₂ можна вважати точковими. Знайдемо енергію системи за допомогою обох формул. Тоді

,

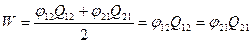де φ₁₂ – потенціал, створений другим зарядом, в місці знаходження першого. Аналогічний зміст має потенціал φ₂₁.

Згідно формули (6.4) ми повинні розбити заряд на нескінченно малі заряди величиною ρdV і кожен з елементів помножити на потенціал, створений не лише іншими кульками, а й елементами даної кульки і, таким чином, результат буде інший.

,

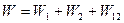де W₁ – енергія взаємодії елементів заряду першої кульки, W₂ – енергія взаємодії елементів заряду першої кульки, W₁₂ – енергія взаємодії елементів заряду першої кульки з елементами заряду другої кульки.

Енергії W₁, W₂ називаються власними енергіями зарядів Q₁ і Q₂ відповідно, W₁₂ – енергія взаємодії зарядів Q₁ і Q₂.

Таким чином, розрахунок енергії за формулою (6.3) дає лише величину W₁₂, а за формулою (6.4) маємо повну енергію взаємодії (разом з власними енергіями зарядів).

Використовуючи формулу (6.4) можна одержати енергію зарядженого провідника і конденсатора.

6.2. Енергія усамітненого зарядженого провідника

Нехай провідник має заряд Q і потенціал φ, оскільки значення потенціалу в усіх точках, де знаходиться заряд однаковий, то його можна винести за знак інтегралу і тоді під інтегралом залишиться лише величина заряду на провіднику ( див. формулу (4)). І враховуючи, що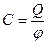

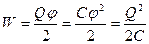. (6.6)

6.3. Енергія зарядженого конденсатора

Нехай Q і φ – заряд і потенціал позитивно зарядженої обкладки конденсатора. Згідно (6.4) потенціальну енергію можна розбити на дві частини для двох обкладок:

.

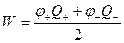Так як Q₊ = - Q_- , то

,

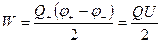U=∆φ – різниця потенціалів на обкладках конденсатора.

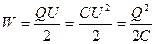. (6.7)

Ці формули визначають повну енергію взаємодії.

Формули (6.6) і (6.7) також справедливі при наявності діелектрика.

6.5. Енергія електростатичного поля

Формула (6.4) визначає електричну енергію будь-якої системи через заряд і потенціал, повну енергію можна також виразити через напруженість електричного поля.

Розглянемо плоский конденсатор, не враховуючи змін поля біля країв пластин (тобто нехтуючи крайовим ефектом). Енергія такого конденсатора визначається формулою (6.7).

.

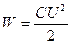Підставимо сюди вираз для ємності плоского конденсатора :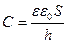

.

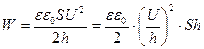Оскільки відношення 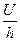є напруженістю електричного поля, а добуток 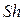– об’єм між простору між обкладками конденсатора, остаточно маємо:

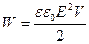. (6.8)

Формула справедлива для однорідного поля, який заповнює об’єм V.

Якщо діелектрик ізотропний, враховуючи, що D=εε₀E можна також записати

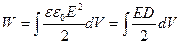. (6.9)

Підінтегральний вираз має зміст енергії поля, яке знаходиться в об’ємі dV, що приводить до ідеї про локалізацію енергії в самому полі. З останніх двох формул слідує, що електрична енергія розподілена в просторі з деякою об’ємною густиною енергії ω.

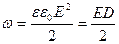. (6.10)

Остання формула справедлива лише для ізотропного діелектрика, для якого виконується співвідношення між поляризованістю і напруженістю зовнішнього поля

.

Лекція 7

Читайте також:

1. Аварійно-рятувальні підрозділи Оперативно-рятувальної служби цивільного захисту, їх призначення і склад.
2. Актив і пасив балансу складаються також з певних розділів.
3. Активи, що реалізуються повільно (А3) – це статті 2-го розділу активу балансу, які включають запаси та інші оборотні активи (рядки 100 до 140 включно, а також рядок 250).
4. Аналіз бойових дій пожежних підрозділів
5. Аналогія величин і рівнянь поступального і обертального руху. Кінетична енергія обертання тіла
6. Б – розділення гелю на дві фази
7. Важливим параметром конденсаторів є пробивна напруга конденсатора. Чим вона більша, тим надійніший конденсатор, тим більша енергія може сконцентруватись на ньому.
8. Взаємодія органів слідства з підрозділами, уповноваженими здійснювати оперативно-розшукову діяльність, при розслідуванні злочинів
9. Взаємодія підрозділів при проведенні виїзних планових та позапланових перевірок
10. Взаємодія СВА з іншими структурними підрозділами підприємства.
11. Взаємодія слідчого з оперативними підрозділами.
12. Визначення та визнання запасів в підрозділах підприємств готельно-ресторанного господарства , їх оцінка та класифікація

Переглядів: 2015