• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

A short theory

A hydrogen atom has one electron which "rotates" in a nuclear field. An electric force on Coulomb attraction acts between the electron and the nucleus. The potential energy of an electron in a nuclear field is

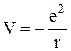, (11.1)

where e is the charge of an electron and r is the distance between the nucleus and electron. Such an atom constitutes a peculiar kind of potential well and is illustrated in fig.11.1.

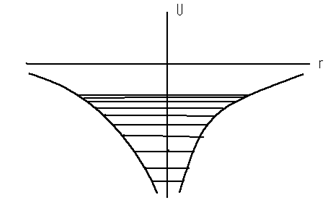
Figure 11.1

The electron inside the atom has a negative potential energy since the minimum value of potential energy tends to infinity when r → 0 and the maximum value is equal to zero. Fig. 11.2 shows the energy levels obtained from the solution of the Schrodinger equation

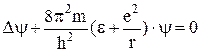. (11.2)

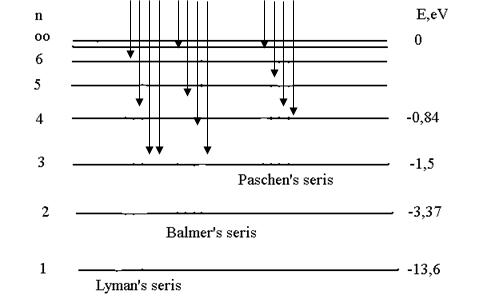Figure 11.2

An important feature of the solution is the drawing together of the levels as the quantum number n increases. The scales of values, which are proportional to energy are given in the units adopted in spectroscopy: volts and reciprocal centimetres. The energy level formula may by written in the form

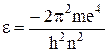. (11.3)

For historical reasons, it is customary to write this formula in the for

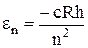, (11.4)

where

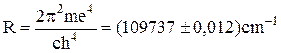(11.5)

is the Rydberg’s constant.

The atomic electron may be located at any one of n levels. The energy of a free hydrogen atom on which no force acts is at the lowest energy level

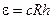, (11.6)

The energy ε = cRh is called the ionisation energy. If the energy imparted to hydrogen atom is less than cRh, a transition of the atom occurs to one of the n levels. Such an atom is said to be in an exited state.

An atom stays in an excited state for a small fraction of a second and then passes to a lower level with the emission off a photon in accordance with the equation

hν_mn = ε_m - ε_n = cRh (1/n² - 1/m²). (11.7)

By calculating for a given n the ν frequencies corresponding to the numbers m = n+1, n+2, ..., we obtain a series of frequencies of lines in the hydrogen spectrum. The series corresponding to n = 2 is known as the Balmer series.

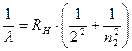. (11.8)

Читайте також:

1. A hand had appeared amongst the flames, groping as though to catch hold of something; a stubby, short-fingered hand covered in ugly old-fashioned rings.
2. A Short Course in Human Relations
3. A Short Course in Human Relations
4. A young witch with short blonde hair poked her head around the curtain; Harry saw that she too was wearing magenta staff robes.
5. A. Make up short dialogues expressing your opinion, agreeing or disagreeing. Use the prompts given below.
6. A. Read the short extract from the interview and recognize any constructions expressing Future Actions.
7. As she named each drink, she gave her short wand a wave, and a cup or glass of it appeared on her desk.
8. B) Give a short description of some other disease using a few phrases from the text above.
9. B. Listen to part of a radio interview with a historian talking about Einstein. Then complete each sentence with a word or a short phrase. (Track 17, CD2)
10. But Mrs. Cole pulled up short, and there was nothing blurry or vague about the inquisitorial glance she shot Dumbledore over her gin glass.
11. Changes of Short Vowels in Early New English

Переглядів: 884