• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Векторний добуток векторів і його властивості. Геометричні застосування векторного добутку.

Упорядкована трійка некомпланарних векторів a, b, c, зведених в одну спільну точку називається правим базисом, якщо з кінця с найкоротший поворот від a lj b видно проти годинникової стрілки. В противному разі трійка векторів називається лівою, або лівим базисом.

Векторним добутком називається вектор c, який записують у вигляді:

c=a*b і якщо задовольня\ться умова:

1) c перпендикул. a, c перпендикул.b

2)| c | = |a |* | b | *sin γ

3) Якщо вектори записують у вигляді а. в. с, то вони повинні утворювати праву трійку векторів:

S_{паралелог.}= | a| | b| sinγ=c

Геометричні властивості:

А) a×b=0 à a || b умова колінеарності векторів

Б) | c | = | a| | b| sin γ= S_{паралелог.}

Алгебраїчні властивості:

1) a × b= -b × a

2) λ a × b = a × λ b

15. Мішаний добуток векторів і його властивості. Обчислення об’ємів паралелепіпеда, призми, пірамід.Необхідна й достатня умови компланарності 3-х векторів

Називається число рівне ( a [ b × c]). Спочатку знаходиться векторний добуток b × c = α , потім скалярний добуток a *α

Геометричні властивості змішаного добутку:

1) Якщо змішаний добуток =0, то вектори a b c компланарні.

2) Об'єм паралелограма побудованого на цих векторах визначається формулою V= | a b c | , при чому змішаний добуток :

( a [ b × c ])= { -V якщо утв. Ліва трійка векторів

{ V якщо утв. Права трійка векторів

Основна алгебраїчна властивість змішаного добутку полягає в тому, що циклічна перестановка векторів не змінює його величини

( a [ b × c ] )= b [ c × a ] = c [ a × b ]

Якщо вектори задані в ортонормованому базисі, то змішаний добуток визначається:

abc = |a_x a_y a_z |

| b_x b_y b_z|

| c_x c_y c_z |

V= .- Об’єм паралелепіпеда

V= - Об’єм трикутної піраміди

Необхідною й достатньою умовою компланарності трьох векторів

є рівність нулю їх мішаного добутку:

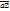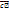( × )× = 0 вектори 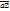, , 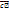компланарні.

5. Якщо ( 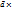)· 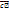> 0 − трійка векторів 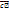, права

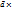
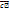( )· < 0 − трійка векторів 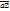, , 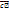ліва.

Читайте також:

1. Effects/Accessories - Ефекти/Аксесуари - Тут ви можете вибрати плагін для застосування його до ландшафту.
2. I. Застосування похідної та інтеграла до роз’язування задач елементарної математики.
3. IV етап. Практичне застосування одержаних даних.
4. IV. ДІЯ ЦЬОГО ЗАКОНУ І ОСОБЛИВОСТІ ЙОГО ЗАСТОСУВАННЯ
5. V. Виконання вправ на застосування узагальнювальних правил.
6. V. Рекомендації щодо безпечного застосування сільськогосподарської техніки при виконанні основних агротехнологічних операцій у рослинництві
7. А) Товар і його властивості.
8. А.1 Стан , та проблемні питання застосування симетричної та асиметричної криптографії.
9. Автомобільні ваги із застосуванням цифрових датчиків
10. Акти застосування норм права
11. Акти застосування норм права в механізмі правового регулювання.
12. Акти застосування юридичних норм: поняття, ознаки, види.

Переглядів: 1631