• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Прочитайте текст и представьте систему действительных чисел в виде предложенной таблицы.

Real Number System

The real number system evolved over time by expanding the notion of what we mean by the word ²number². At first, ²number² meant something you could count. These are called the natural numbers, or sometimes the counting numbers.

Natural Numbers or ²Counting Numbers² are 1, 2, 3, 4, 5 . . . (The use of three dots at the end of the list is a common mathematical notation to indicate that the list keeps going ad infinitum.)

At some point, the idea of ²zero² came to be considered as a number. We call the set of natural numbers plus the number zero the whole numbers.

Whole Numbers arenatural numbers together with ²zero², 1, 2, 3, 4, 5 . . . Even more abstract than zero is the idea of negative numbers. It took longer for the idea of negative numbers to be accepted, but eventually they came to be seen as something we could call ²numbers². The expanded set of numbers that we get by including negative versions of the counting numbers is called the integers.

Integers - whole numbers plus negatives. Ex. . . . –4, –3, –2, –1, 0, 1, 2, 3, 4. . . How can you have less than zero? Well, do you have a checking account? Having less than zero means that you have to add some to it just to get it up to zero. And if you take more out of it, it will be even further less than zero, meaning that you will have to add even more just to get it up to zero.

The next generalization that we can make is to include the idea of fractions. While it is unlikely that a farmer owns a fractional number of sheep, many other things in real life are measured in fractions, like a half-cup of sugar. If we add fractions to the set of integers, we get the set of rational numbers.

Rational Numbers - all numbers of the form , where a and b are integers (but b cannot be zero.)

Rational numbers include what we usually call fractions. (Notice that the word ²rational² contains the word ²ratio², which should remind you of fractions.)

The bottom of the fraction is called the denominator.(The denominator cannot be zero! But the numerator can.) Think of it as the denomination - it tells you what size fraction we are talking about: fourths, fifths, etc. The top of the fraction is called the numerator. It tells you how many fourths, fifths, or whatever.

Fractions can be numbers smaller than 1, like 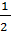or (called proper fractions), or they can be numbers bigger than 1 (called improper fractions), like two-and-a-half, which we could also write as . All integers can also be thought of as rational numbers, with a denominator of 1: 3 = This means that all the previous sets of numbers (natural numbers, whole numbers, and integers) are subsets of the rational numbers.

Now it might seem as though the set of rational numbers would cover every possible case, but that is not so. There are numbers that cannot be expressed as a fraction, and these numbers are called irrational because they are not rational.

Читайте також:

1. I. Почитайте и переведите текст
2. I. Прочитайте и переведите текст
3. I. Прочитайте и переведите текст.
4. I. Прочитайте и переведите текст.
5. I. Прочитайте и переведите текст.
6. I. Прочитайте и переведите текст.
7. II. Множення круглих багатоцифрових чисел на розрядні числа.
8. II.5. Анотування і реферування текстів; анотаційний та реферативний переклад
9. III ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДРУГУЮ
10. III. Аудіювання тексту з метою розуміння
11. III.4 Форматування тексту.
12. N – чисельність популяції

Переглядів: 417