
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
ТЕМА 5. СТАТИСТИЧНЕ ВИВЧЕННЯ ЗВ'ЯЗКУ МІЖ ЯВИЩАМИ
.
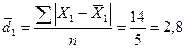 шт.
шт.
 шт.
шт.
Отже, СЛВ в першій бригаді в 2,3 рази більше, ніж у другій, що теж свідчить про те, що за ознакою продуктивності праці склад першої бригади менш однорідний чим другої.
Варіаційний розмах і СЛВ були єдиними вимірниками варіації на початку розвитку теорії статистики.
Зараз, у міру розвитку математичної статистики, замість СЛВ частіше використовують середній квадрат відхилень так звану дисперсію  і середнє квадратичне відхилення
і середнє квадратичне відхилення  (його ще називають – стандартне відхилення).
(його ще називають – стандартне відхилення).
Дисперсія являє собою середню величину з квадратів відхилень окремих значень ознаки від їх середньої арифметичний.
Дисперсія визначається за такою формулою:
проста 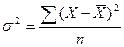 ;
;
зважена  .
.
Таким чином, дисперсія виражає міру ступеня коливанності досліджуваної ознаки. Вона враховує знак відхилення і на відміну від СЛВ не має розмірності.
Середнє квадратичне відхилення являє собою корінь квадратний з дисперсії.
Необхідність його обчислення пов'язана з тим, що розмірність дисперсії дорівнює квадрату розмірності досліджуваної ознаки. Це робить її не завжди придатною і зручною при визначенні міри ступеня коливанності ознаки, для чого і використовується СКВ.
Просте СКВ визначається за формулою: 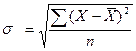 .
.
Зважене:  .
.
Порядок розрахунку 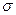 такий.
такий.
1. Визначається середня арифметична  .
.
2. Обчислюються відхилення від середньої 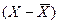 .
.
3. Обчислюється квадрат відхилень 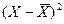 .
.
4. Обчислюється сума квадратів відхилень 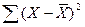 .
.
5. Обчислюється середній квадрат відхилень (дисперсія) 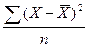 .
.
6. Обчислюється СКВ 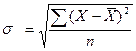 .
.
Зміст СКВ такий ж, як і СЛВ – чим менше 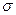 , тим однорідніша сукупність, тим типовіша середня, тим стійкіше явище і процес.
, тим однорідніша сукупність, тим типовіша середня, тим стійкіше явище і процес.
СКВ завжди більше СЛВ. У симетричних чи помірно асиметричних розподілах  , і
, і 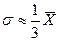 .
.
При розв’язанні практичних задач варто мати на увазі, що СЛВ вимірює й узагальнює відхилення від середньої, не вносячи нічого такого, що не пов'язано з абсолютними розмірами відхилень. СКВ і дисперсія, тим часом, відносячи відхилення до квадрату зменшують питому вагу малих відхилень і збільшують питому вагу великих відхилень у загальній сумі відхилень.
Тобто структура лінійного відхилення краще відображає реальні відхилення, ніж структура квадратичного відхилення.
ПРИКЛАД.
Продуктивність праці робітників
| Табель-ний номер робітника | 1-я бригада | 2-я бригада | ||||

|

|

|
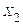
|
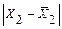
|
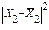
| |
| Разом: |
 .
.
 .
.
Бачимо, що дисперсія у 1-й бригаді більш ніж у 4 рази більша, ніж у другій.
Середнє квадратичне відхилення складе по бригадах:
 (шт.);
(шт.);
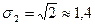 (шт.).
(шт.).
Таким чином, середнє квадратичне відхилення в першій бригаді за продуктивністю праці більш ніж у 2 рази більше, ніж у другій.
Середнє квадратичне відхилення, варіаційний розмах і середнє лінійне відхилення завжди виражаються в іменованих одиницях, тобто у тих же, що і досліджувана ознака (гривнях, тонах, літрах і т.д.). Ці показники показують, на скільки у середньому, відхиляються конкретні варіанти ознаки від середньої її величини.
Саме собою зрозуміло, що стосовно до інтервального ряду, розрахунок СКВ пов'язаний із необхідністю визначення центру інтервалу.
Для обчислення дисперсії і СКВ зручно користуватися наступними математичними властивостями дисперсії:
1. Якщо всі значення ознаки, що варіює, зменшити на постійну величину, дисперсія не зміниться.
2. Якщо всі значення варіантів зменшити в k раз, дисперсія зменшиться в k2 разів.
3. Дисперсія дорівнює середньої з квадратів варіантів мінус квадрат середньої:
 ,
,
 ,
,
де  – для зваженої дисперсії;
– для зваженої дисперсії;
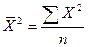 – для простої,
– для простої,
тобто  – проста;
– проста;
 – зважена.
– зважена.
Для порівняння варіації розмаху ознак у різних сукупностях (коли показники варіації виражені в різних одиницях) використовується відносний показник, так званий коефіцієнт варіації  .
.
Він являє собою відсоткове відношення середнього квадратичного відхилення до середньої арифметичної:
 .
.
Коефіцієнт варіації характеризує коливанність ознаки у відносних одиницях виміру.
За допомогою цього коефіцієнту можна порівнювати варіацію таких різних ознак як продуктивність праці, врожайність, продуктивність тваринництва і т.д.
У нашому прикладі коефіцієнт варіації по продуктивності праці робітників у двох бригадах складає:
по першій бригаді – 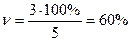 ,
,
по другій бригаді – 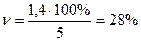 .
.
При однаковій продуктивності праці (25 деталей у зміну) показники варіації в першій бригаді більші. Це значить, що склад робітників у ній більш «строкатий», більш різнорідний. Отже, у неї є резерви для підвищення продуктивності праці. У другій бригаді склад робітників по продуктивності праці більш однорідний, тобто сукупність більш однорідна за складом. Сукупність вважається однорідною, якщо 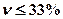 .
.
5.1 Взаємозв'язки суспільних явищ і необхідність їхнього статистичного вивчення
5.2 Види і форми взаємозв'язку між явищами
5.3 Основні прийоми і методи вивчення взаємозв'язків
5.4 Поняття про кореляційно-регресійний аналіз
5.5 Щільність зв'язку і найпростіші методи її виміру
Відомо, що всі явища і процеси, що відбуваються у природі і суспільстві, так чи інакше зв'язані між собою, залежать один від одного.
Так, результати діяльності промисловості залежать від роботи інших галузей народного господарства: енергетики, сільського господарства, транспорту та ін.
У свою чергу результати діяльності того ж сільського господарства в значній мірі залежать від промисловості, яка постачає йому машини, добрива, засоби захисту рослин і т. ін.
Взаємозв'язок і взаємозалежність виявляються і у роботі будь-якого підприємства, організації чи закладу.
Без вивчення взаємозв'язків, їхнього характеру, сили та інших особливостей, неможливо керувати явищами і прогнозувати їхній розвиток.
Тому однієї з найважливіших задач аналізу статистичних даних є задача встановлення і пояснення взаємозв'язків, їх виміру і кількісного вираження.
Економісту у процесі своєї діяльності практично постійно приходиться мати справа з взаємозалежними показниками.
Так, наприклад, він повинний вивчати динаміку зарплати у зв'язку з динамікою продуктивності праці. Динаміку продуктивності праці у зв'язку з динамікою собівартості продукції, а динаміку собівартості у залежності від обсягу продукції і т.ін.
Причому, основна задача економіста не в тому, щоб просто проілюструвати різні сфери діяльності підприємства (організації) за допомогою цифр. Він повинний за допомогою аналізу цифрових показників виявити «вузькі місця» у роботі підприємства, розкрити причини та умови, що впливають на результати роботи.
Економічний аналіз залежності процесів і явищ дозволить намітити необхідні заходи для поліпшення тих чи інших сторін діяльності підприємства. Тільки у цьому випадку робота економіста не буде виглядати простою констатацією наявних фактів.
Вивчення явищ у їх взаємозв'язку означає, насамперед, вивчення причинно-наслідкової залежності між ними. Тому, що одне явище завжди являє собою причину, а інше – наслідок, тобто результат дії цієї причини.
Відповідно і ознаки, що характеризують явище причини, називаються факторними (незалежними) ознаками, а ознаки, що характеризують явище наслідку – результатними (залежними).
Між причиною і наслідком часто існує взаємодія. Тобто наслідок може, у свою чергу, впливати на причину.
НАПРИКЛАД, виробництво – необхідна передумова для споживання, а споживання – наслідок виробництва. Споживання ж, у свою чергу, впливає на виробництво визначаючи його обсяг, асортимент і якість продукції.
За характером залежності між факторними і результатними ознаками зв'язки підрозділяються на:
– функціональні або строго детерміновані (від латинського determinatio – обмеження, визначення), тобто строгі, повні;
– стохастичні, тобто імовірні, нестрогі.
Функціональні – це зв'язки, при яких кожному значенню факторної ознаки (аргументу) відповідає одне або декілька строго визначених значень результатної ознаки (функції).
Тобто при функціональному зв'язку зміна значення результатної ознаки цілком залежить від зміни значення факторної ознаки.
Такі зв'язки спостерігаються переважно у точних науках: математиці, фізиці, хімії, астрономії, тобто вони притаманні, в основному, фізичним і хімічним явищам.
НАПРИКЛАД, площа круга і довжина кола цілком залежать від зміни радіуса, швидкість падіння від висоти і т.ін. Або, якщо 
 , те значенню
, те значенню  , відповідають два строго визначених значення:
, відповідають два строго визначених значення:  .
.
Стохастичні – це зв'язки, при яких кожному значенню факторної ознаки відповідає безліч значень результатної ознаки, що варіюють і не мають строго визначеної залежності від зміни величини факторної ознаки.
Інакше кажучи, зміна факторної ознаки приводить не до строго визначеної зміни результатної ознаки, а до зміни тільки розподілу його значень.
Окремим випадком стохастичних зв'язків є кореляційні (статистичні). Це зв'язки, при яких кожному значенню факторної ознаки  відповідає середнє значення результатної ознаки
відповідає середнє значення результатної ознаки  .
.
Тобто кореляційний зв'язок виявляється у вигляді тенденції (загального напрямку) змін середніх значень результатної ознаки у залежності від змін факторної ознаки.
Саме такого роду зв'язки переважають у соціально-економічних явищах і процесах. У них, як правило, немає строгої залежності між причиною і результатом. Це пов'язано з тим, що соціально-економічні явища являють собою результат одночасного впливу безлічі причин і умов.
Тому при вивченні цих явищ необхідно виявляти основні з цих причин, абстрагуючи від малозначимих, другорядних.
НАПРИКЛАД, кількість деталей, вироблених робітником на верстаті залежить від багатьох причин: кваліфікації робітника, налагодження верстата і ступеня його зносу, дисциплінованості і самопочуття робітника, організації праці і т.д.
Кореляційні зв'язки є нестрогими, неповними, імовірними і виявляються тільки у середніх величинах при наявності наступних умов:
1. Якщо є дані по досить великій сукупності явищ. Вважається, що число спостережень повинне не менш ніж у 5 разів перевищувати число досліджуваних факторів.
2. Якщо закономірність, що виявляється в даному явищі, надійно виражена у середній величині.
Саме слово «кореляція» ввів у статистику англійський біолог і статистик Френсіс Гальтон наприкінці XIX століття. У перекладі з англійського воно означає «відповідність, співвідношення». Причому під цим розумівся не просто зв'язок – relation, а як би зв'язок – correlation, тобто зв'язок, але не у звичній функціональній формі. Ф.Гальтон і К.Пірсон вважаються основоположниками теорії кореляції.
У зв'язку з тим, що функціональні зв'язки в соціально-економічних явищах зустрічаються рідко, а переважають, як підкреслювалося вище, кореляційні, то саме їх вивченням і займається статистика.
Кореляційні зв'язки за напрямком бувають прямими і оберненими.
Прямим називається зв'язок, при якому із збільшенням факторної ознаки збільшується і результатна.
Оберненим називається зв'язок, при якому із збільшенням факторної ознаки – результатна зменшується.
За аналітичним вираженням кореляційні зв'язки підрозділяються на прямолінійні (лінійні) і нелінійні (криволінійні).
Лінійним називається зв'язок, який можна приблизно виразити рівнянням прямої лінії.
Нелінійним є зв'язок, що може бути вираженій рівнянням якої-небудь кривої лінії (параболи, гіперболи, показової, степеневої функції й ін.).
Кореляційні зв'язки можуть бути також різного ступеня щільності. Якщо значенню факторної ознаки  відповідають близькі один одному (тісно розташовані біля своєї середньої) значення результатної ознаки
відповідають близькі один одному (тісно розташовані біля своєї середньої) значення результатної ознаки  – зв'язок є щільний.
– зв'язок є щільний.
Якщо ж значення результатної ознаки, при тому самому значенні факторного варіюють (змінюються) значно – зв'язок менш щільний.
Для виявлення наявності зв'язку, його форми і напрямку в статистиці використовуються різні методи:
– метод зіставлення паралельних рядів;
– графічний;
– аналітичних груповань;
– кореляційно-регресійного аналізу (КРА).
Розглянемо суть кожного з них.
Метод зіставлення паралельних рядів – грунтується на зіставленні отриманих у результаті зведення статистичних показників у вигляді двох і більш паралельних рядів.
Таке зіставлення дозволяє установити наявність зв'язку і його напрямок.
НАПРИКЛАД:
| Х | ||||||
| У1 | ||||||
| У2 |
Де Х – розряд робітника;
У1 , У2 – виробіток.
Зіставляючи показники, бачимо, що із збільшенням факторної ознаки (Х), значення результатної ознаки (У1) також зростають. Отже, має місце прямий зв'язок між двома цими показниками.
Графічний метод – дозволяє виявити наявність зв'язку двох ознак за допомогою побудови і аналізу поля кореляції.
Для цього в системі координат на осі абсцис відкладаються значення факторної ознаки, а на осі ординат – результатної. Одержимо деяке розсіювання безлічі точок – так зване кореляційне поле.
По розташуванню точок у кореляційному полі можна зробити висновок про наявність зв'язку, його напрямок і щільність.
 У
У

× × × × × × ×
× × × × × × ×
× × ×
× ×
× × × × × ×
× × × × × × ×
× × × × ×
× × × ×
× × ×
× × ×

0 Х
Рис. 1 Приклад прямого зв'язку
 У
У
× ×
× × ×
× × ×
× × ×
× × ×
× × ×
× × ×
× × × ×
× × ×
× × ×
× ×

0 Х
Рис.2 Приклад оберненого зв'язку
Якщо точки розташовані знизу, праворуч, нагору – зв'язок прямий (рис. 1). Якщо ж зверху від осі ординат, праворуч, униз – зв'язок обернений (рис. 2).
Чим сильніший зв'язок між ознаками, тим щільніше будуть розташовуватися точки кореляційного поля навколо визначеної лінії, що виражає форму зв'язку (рис. 1).
Метод аналітичних груповань схематично можна представити таким чином:
1. Спочатку всі одиниці сукупності розбивають на певну кількість груп за зростанням факторної ознаки, тобто ознаки, покладеної в основу угруповання.
2. Потім по кожній групі розраховується середня величина результатної ознаки.
3. Якщо із зростанням факторної ознаки, при переході від групи до групи, відбувається зростання або убування результатної ознаки, значить можна зробити висновок про наявність зв'язку і його напрямок.
Пояснити викладене можна на ПРИКЛАДІ вивчення зв'язків між стажем роботи і годинною зарплатою в колективі робітників однієї професії з 50 чоловік.
Насамперед з'ясуємо: чи повинний бути зв'язок між стажем роботи і годинною заробітною платою?
Теоретичний аналіз приводить до логічного висновку: такий зв'язок повинний бути. Адже із збільшенням стажу підвищується кваліфікація робітника, збільшується кількість і поліпшується якість вироблюваних ним виробів і, відповідно, повинна підвищуватися зарплата.
Для підтвердження наших припущень наведемо і розглянемо конкретні дані про значення ознак які нас цікавлять для окремих робітників.
Для прикладу візьмемо відомості про десять робітників з різним стажем роботи.
| стаж | Годинна зарплата, грн. | стаж | Годинна зарплата, грн.. |
| 3,0 | 4,8 | ||
| 4,0 | 6,4 | ||
| 3,4 | 6,5 | ||
| 4,0 | 6,2 | ||
| 3,8 | 8,0 |
Наскільки можна судити з наведених даних, зв'язок між стажем і годинною заробітною платою начебто є. Однак не у всіх робітників із збільшенням стажу збільшилася і годинна зарплата. Це зв'язано з тим, що на величину зарплати впливає не тільки стаж, але і ряд інших факторів: освіта, технічна підготовка, дисципліна, здоров'я і ін.
Нас же цікавить, насамперед, вплив стажу. Тому згрупуємо робітників за стажем в порядку його зростання. При цьому можна припустити, що у всіх групах інші фактори, що впливають на зарплату, діють приблизно однаково.
| Групи робітників за стажем | Число робітників | Загальна сума годинної зарплати, грн. | Середня годинна зарплата, грн. |
| 0 – 6 | 25,2 | 3,6 | |
| 6 – 12 | 85,0 | 5,0 | |
| 12 – 18 | 83,6 | 6,0 | |
| 18 – 24 | 43,2 | 7,2 | |
| 24 – 30 | 44,6 | 7,4 | |
| Разом: | 282,0 | 5,6 |
Розрахувавши середню годинну зарплату по кожній із груп бачимо, що із збільшенням стажу середня годинна зарплата збільшується.
Отже, між стажем роботи і розміром годинної зарплати існує зв'язок (залежність).
Тепер нас цікавить питання: а які ж характер, форма і ступінь цієї залежності (зв'язку)?
На це питання найбільше точно може відповісти метод кореляційного аналізу. Тільки він один, на відміну від всіх інших методів, дозволяє установити єдину міру зв'язку, її силу і щільність.
Саме тому метод кореляційного аналізу займає в даний час ведуче місце серед всіх названих вище методів.
Його роль особливо зросла у зв'язку із широким впровадженням у практику аналітичної роботи швидкодіючих ЕОМ і ПЕОМ, що мають набір стандартних програм кореляційного аналізу, які дозволяють оперативно вирішувати задачі вивчення статистичних зв'язків.
| <== попередня сторінка | | | наступна сторінка ==> |
| Показники варіації | | | Основні поняття і задачі кореляційного аналізу |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |