
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Показники варіації
Мода
Поняття «Мода» у статистику ввів К. Пірсон.
Модою (Мо ) у статистиці іменується поняття, що має той же зміст, що і мода у звичайному розумінні цього слова. Тобто у побуті модним платтям чи фасоном називається те, що має найбільш широке поширення в даний момент.
У статистиці модою(Мо) називається таке значення варіюючої ознаки, яка найбільш часто зустрічається серед одиниць даної сукупності.
Тобто, мода – це найбільш типове, характерне для даної сукупності значення ознаки (варіанта). Так, у варіаційному ряді розподілу міст за числом заводів, що ми приводили вище як приклад, мода дорівнює 3. Саме таке число заводів має найбільше поширення серед міст даного ряду. Таких міст найбільше число – 4.
Таким чином, для дискретного ряду, як у нашому прикладі, мода – це варіант, що має найбільшу частоту, тобто найчастіше зустрічається. Визначення її здійснюється без всяких розрахунків, шляхом простого перегляду стовпця частот. Дивлячись на цей стовпець, варто лише знайти найбільше число в ньому. Йому і відповідає значення варіанта (ознаки), що і є модою.
У випадку ж з інтервальним рядом, визначення моди вимагає розрахунків і здійснюється в наступній послідовності:
1. Шляхом перегляду стовпця частот визначають інтервал, у якому знаходиться мода, тобто модальний інтервал. При цьому, у варіаційному ряді з рівними інтервалами модальний інтервал визначається за найбільшою частотою. У рядах з нерівними інтервалами – за найбільшою щільністю розподілу. Тобто, у цьому випадку необхідно розрахувати ще стовпець щільності розподілу.
Щільність розподілу, як нам уже відомо, розраховується шляхом ділення частоти на величину відповідного інтервалу, тобто  .
.
2. За формулі визначається мода:
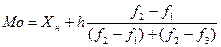 ,
,
де 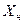 – нижня границя модального інтервалу;
– нижня границя модального інтервалу;
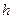 – величина модального інтервалу;
– величина модального інтервалу;
 – частота передмодального інтервалу;
– частота передмодального інтервалу;
 – частота модального інтервалу;
– частота модального інтервалу;
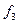 – частота післямодального інтервалу.
– частота післямодального інтервалу.
ПРИКЛАД: визначимо моду розглянутого вище інтервального ряду розподілу сіл району за кількостю населення.
1. Переглянувши стовпець частот бачимо, що Мо знаходиться в інтервалі 300 – 400, йому відповідає найбільша частота.
2. За формулою:
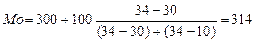 (чіл).
(чіл).
Можна зробити висновок, що найбільш типовим селом у районі є село з кількістю жителів 314 чоловік.
Мо як і Ме є описовою характеристикою сукупностей з кількісно варіюючими ознаками і не може замінити середню узагальнюючу величину. Вона, як і середня, теж типова величина, але, на відміну від середньої характеризує величину ознаки, властиву хоч і значній частині сукупності, але не всій сукупності в цілому.
Мо, насамперед відповідає на запитання про те, яке значення досліджуваної ознаки найбільше ймовірно.
Якщо в якомусь розподілі два варіанти виділяються відносно великими (рівними) частотами, то такий розподіл має дві моди і називається двомодальним.
При вирішенні практичних задач Мо використовується, наприклад, при:
– плануванні обсягу виробництва того чи іншого товару (урахування попиту);
– визначенні цін на ринках на той чи інший продукт;
– визначенні потоку пасажирів у міському транспорті (який маршрут, який вид транспорту);
– визначенні потоку покупців у магазинах і т.п.
Середні величини, як ми уже відзначили, відіграють найважливішу роль в економіко-статистичному аналізі. Їх розрахунок дає можливість охарактеризувати не тільки всю досліджувану сукупність у цілому, але і її окремі елементи.
Разом з цим, визначивши середню арифметичну, наприклад, ми ще не можемо з впевненістю сказати наскільки добре вона характеризує всю сукупність.
Як виглядають щодо середньої окремі значення досліджуваної ознаки? Далеко чи близько відхиляються вони від неї, тобто як вони варіюють?
Бувають випадки, коли середні величини двох чи більш сукупностей однакові, але істотно розрізняються своєю варіацією.
Так, в одній сукупності окремі варіанти можуть далеко відстояти від своєї середньої:  , а в іншій – розташовуватися більш близько (купчасто) навколо її:
, а в іншій – розташовуватися більш близько (купчасто) навколо її:  .
.
Зрозуміло, що в останньому випадку середня величина краще представляє (характеризує) досліджувану сукупність.
Тому, якщо ми претендуємо на серйозність аналізу і виявлення закономірностей, не можна обмежуватися обчисленням тільки середніх величин.
Необхідно мати ще і такі показники, що характеризували б відхилення окремих значень ознак від середньої величини.
Для цього в теорії статистики використовуються показники варіації які дають для аналізу не менш коштовну інформацію, чим середні величини. В економіці вони потрібні, наприклад, для характеристики ступеня ритмічності роботи підприємства.
Варіацією, тобто коливанням, зміною ознаки називається розходження його значень у різних одиниць сукупності у той самий момент чи період часу.
Показниками варіації в статистиці є:
1. Варіаційний розмах (амплітуда коливань).
2. Середнє лінійне відхилення.
3. Середній квадрат відхилень (дисперсія).
4. Середнє квадратичне відхилення (стандартне відхилення).
5. Коефіцієнт варіації.
Варіаційний розмах (амплітуда коливань) є найбільш простим показником варіації ознаки. Обчислюється як різниця між найбільшим і найменшим значеннями кількісної ознаки в деякій сукупності.
 ,
,
де 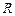 – розмах варіації,
– розмах варіації,
 – найбільше значення ознаки,
– найбільше значення ознаки,
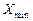 – найменше значення ознаки.
– найменше значення ознаки.
ПРИКЛАД: є дані про продуктивність праці робітників у двох бригадах.
| Табельний номер | Вироблено продукції за зміну, шт. (х) | |
| 1-я бригада | 2-я бригада | |
| Разом: |
Середня продуктивність праці в обох бригадах однакова: 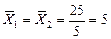 .
.
Однак у першій бригаді варіація продуктивності праці більша, ніж у другій. Отже, можна сказати, що перша бригада за своїм складом у відношенні ознаки продуктивності праці менш однорідна, чим друга.
Для виміру ступеня варіювання даної ознаки визначимо розмах варіації.
Для 1-й бригади:  шт.
шт.
Для 2-й бригади: 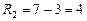 шт.
шт.
Бачимо, що і варіаційний розмах ознаки продуктивності праці в першій бригаді в два рази більший, ніж у другій.
Простота обчислення розмаху варіації сприяє його широкому використанню в теоретичних дослідженнях і практичних розрахунках.
Разом з тим, цей показник має істотний недолік: він не дає представлення про ступінь коливанності ознаки всередині сукупності, тому що обчислюється на основі тільки двох крайніх значень ознаки, які не завжди характерні і можуть носити випадковий характер.
Тому існує інший показник, що дає більш точну характеристику коливанності ознаки, тому що порівнює всі наявні його значення із середньою величиною.
Цей показник називається середнє лінійне відхилення  .
.
Воно являє собою середню арифметичну з відхилень окремих абсолютних значень ознаки від їхнього середнього значення. Може бути простим і зваженим.
Просте середнє лінійне відхилення (СЛВ) обчислюється по формулі:
 ,
,
де 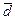 – середнє лінійне відхилення;
– середнє лінійне відхилення;
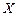 – конкретне значення варіанта ознаки;
– конкретне значення варіанта ознаки;
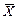 – середнє значення ознаки;
– середнє значення ознаки;
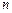 – число варіантів.
– число варіантів.
Обчислення СЛВ здійснюється в наступній послідовності:
1. Визначається середнє значення ознаки  .
.
2. Зі значення кожного варіанта віднімають середню, визначаючи відхилення від середньої 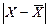 .
.
3. Абсолютну суму відхилень поділяють на число варіантів 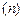 .
.
Для варіаційного ряду обчислюють СЛВ зважене:
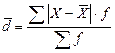 .
.
ПРИКЛАД.
| Табельний номер робітника | 1-я бригада | 2-я бригада | ||||

|
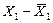
|

|

|
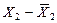
|

| |
| -4 | -2 | |||||
| -3 | -1 | |||||
| Разом: |
Читайте також:
- IV група- показники надійності підприємства
- Абсолютні показники фінансової стійкості
- Абсолютні показники фінансової стійкості та її типи
- Абсолютні та відності показники результатів діяльності підприємства.
- Аналітичні показники динаміки та прийоми їх обчислення
- Аналітичні показники ряду динаміки.
- Аналітичні показники ряду динаміки.
- Базисні показники
- Варіації факторів виробництва та оптимум товаровиробника
- Вартісні показники обсягу виробництва.
- Вартісні показники продукції сільського господарства
- Види і показники зношення основних фондів
| <== попередня сторінка | | | наступна сторінка ==> |
| Структурні середні | | | ТЕМА 5. СТАТИСТИЧНЕ ВИВЧЕННЯ ЗВ'ЯЗКУ МІЖ ЯВИЩАМИ |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |