
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Структурні середні
Поряд з розглянутими вище різновидами середніх величин як додаткові характеристики варіаційних рядів розраховуються так звані структурні (порядкові) середні: медіана і мода.
Назва медіани взята з геометрії, де медіаною називається відрізок, що з'єднує одну з вершин трикутника із серединою протилежної сторони і поділяє сторону на дві рівні частини.
У статистиці Ме також поділяє на дві рівні частини площу гістограми розподілу. Вона являє собою значення центрального елементу ранжируваного ряду.
Тобто, Ме – значення ознаки, що розташоване в середині ранжируваної сукупності і поділяє сукупність на дві рівні частини - із значеннями ознаки менше і більше медіани.
Поняття Ме легко усвідомити на наступному простому ПРИКЛАДІ: є група студентів із семи чоловік.
Необхідно охарактеризувати структуру даної сукупності за ознакою віку, якщо він варіює таким чином:
18 19 17 20 18 24 21.
Це можна зробити в такий спосіб: визначити середній вік студента, як середню арифметичну, і подивитися структуру сукупності щодо середньої.
Тобто, подивитися скілько чоловік мають вік менше середньої по групі і скільки більше:
 років.
років.
Але можна зробити це і за допомогою медіани, визначивши її значення.
Щоб визначити медіану необхідно:
1) на основі даної сукупності побудувати ранжируваний ряд і пронумерувати його члени;
2) якщо число членів ряду непарне – додати до цього числа одиницю і розділити на 2, тобто  .
.
У результаті одержимо порядковий номер члена ряду із значенням ознаки рівним медіані.
3) якщо ж число членів ряду парне, то медіану визначають як середню арифметичну з 2-х центральних елементів ряду.
У нашому ПРИКЛАДІ:
| |
| Вік | |||||||
| Порядковий № за віком | 
|
Нолмер Ме  . Цьому порядковому номеру відповідає значення ознаки рівне 19.
. Цьому порядковому номеру відповідає значення ознаки рівне 19.
Отже, значення Ме для даної сукупності дорівнює 19 років.
Дійсно, це центральний елемент ранжируваного ряду, тому що він поділяє сукупність на дві рівні частини: ліворуч від нього три студенти молодше 19 років, а праворуч три студенти старше 19 років.
Приведений приклад визначення Ме відноситься до незгрупованих даних.
Практично ж Ме розраховують, як правило, для сукупностей, представлених у вигляді дискретного чи інтервального ряду.
У цих випадках використовують накопичені частоти.
Під накопиченими частотамирозуміють наростаючий підсумок послідовного підсумовування частот починаючи з першого варіанту чи першого інтервалу.
Для дискретного ряду Ме визначається без особливих розрахунків у наступній послідовності:
1. Визначаються накопичені частоти, тобто додатково будується стовпець накопичених частот.
2. Розділивши суму частот на два визначаємо порядковий номер Ме.
3. Перша із накопичених частот, яка більша, або дорівнює номеру Ме, вкаже на значення медіани у стовпчику варіантів.
ПРИКЛАД: у наведеному вже прикладі розподілу міст за числом заводів визначимо Ме.
| Число заводів (х) | Число міст (f) | Накопичені частоти (S) | ||
| 5 (2+3) | |||
| Ме 3 | 9 (5+4) | |||
| Разом: |
1. Порядковий номер № Ме = 12:2 = 6.
2. По накопичених частотах бачимо, що перша із накопичених частот, яка більша номера Ме дорівнює 9, їй відповідає значення варіанту 3 у стовпчику варіантів. Значить 3 і буде Ме .
Для інтервального ряду порядок обчислення Ме такий:
1. По сумі частот визначається порядковий номер Ме .
2. По накопичених частотах визначається медіанний інтервал, тобто інтервал, у якому знаходиться Ме .
3. За формулою визначається медіана:
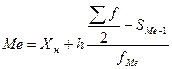 ,
,
де 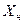 – нижня границя медіанного інтервалу;
– нижня границя медіанного інтервалу;
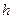 – величина медіанного інтервалу;
– величина медіанного інтервалу;
 – порядковий номер Ме ;
– порядковий номер Ме ;
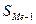 – накопичена частота до медіанного інтервалу;
– накопичена частота до медіанного інтервалу;
 – частота медіанного інтервалу.
– частота медіанного інтервалу.
Ме , як видно зі способів її обчислення, не залежить від двох крайніх значень ряду.
Якщо крайні значення ряду надмірно великі чи малі, тобто нетипові, чи ряд містить відкриті інтервали, то Ме може дати більш точне уявлення про середню, чим середня арифметична, оскільки на неї не впливають ці нетипові значення ознаки.
Крім того, медіана, на відміну від середньої, не є абстрактною величиною. Вона знаходиться точно в середині ранжируваного ряду і являє собою реальне значення ознаки особливо у випадку непарного числа одиниць сукупності.
Як самостійна величина Ме використовується, як правило, при вирішенні деяких задач, пов'язаних з визначенням оптимуму, що збігається з варіантом, який припадає на середину ряду.
НАПРИКЛАД:
– оптимальне розміщення водопровідної колонки на вулиці, таким чином, щоб загальна відстань до неї для мешканців була мінімальною;
– оптимальне розміщення цукрових заводів, ощадбанків, баз, магазинів, пунктів прийому склотари і т.ін.
Разом з тим, не применшуючи значення Ме в аналізі слід зазначити, що вона є все-таки не основною, а додатковою характеристикою сукупності.
Основною характеристикою сукупності є середня величина, що узагальнює всі значення ознаки і представляє собою центр розподілу відхилень значень ознаки від рівнодіючої.
Величина Ме , як правило, відрізняється від величини середньої і може збігатися з нею тільки у випадку симетрії варіаційного ряду.
Розглянемо обчислення Ме на наступному прикладі.
ПРИКЛАД: є інтервальний ряд розподілу сіл Сумського району за кількостю проживаючого у них населення. Причому, межі відкритих крайніх інтервалів даного ряду невідомі. Величина середньої арифметичної дасть у цьому випадку менш точний показник, ніж Ме .
| Населення, чол. (х) | Кількість сіл (f) | Накопичені частоти (S) | ||
| до 100 | ||||
| 100 – 200 | ||||
| ||||
Мо | ||||
| 400 – 500 | ||||
| понад 500 | ||||
| Разом: |
1. Визначаємо порядковий номер № Ме = 100 : 2 = 50.
2. По накопичених частотах бачимо, що 50-тй номер елементу ряду знаходиться в інтервалі 200 – 300.
3. За формулою:
 (чол.).
(чол.).
Отже, можна зробити висновок:
– у половині сіл району проживає менше 287 чоловік, а в половині більше 287 чоловік.
Читайте також:
- А середній коефіцієнт росту в такому випадку визначається як
- Абсолютні, відносні та середні величини.
- Види злочинів за безпосереднім об'єктом
- Види середніх величин
- Види середніх величин та способи їх обрахування.
- Види середніх величин та способи їх обрахування.
- Види середніх і способи їх обчислення
- Визначення середніх значень динамічних рядів
- Визначення середнього абсолютного приросту середніх темпів зростання і приросту
- Витрати виробництва та їх структура. Суть, види витрат. Закон спадної віддачі. Середні та граничні витрати.
- Вищий середній нижчий
- Вищий, середній, нижчий
Переглядів: 1104
| <== попередня сторінка | | | наступна сторінка ==> |
| Середня геометрична | | | Показники варіації |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |