
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Середня геометрична
Природу і сутність середньої геометричної найкраще можна пояснити на наступному простому прикладі.
ПРИКЛАД: нехай є два числа: 4 і 16. Середня арифметична з них дорівнює 10. Число 10 на стільки ж більше 4, на скількох воно менше 16: 4 < 10 < 16.
Нам потрібно знайти число, яке буде в стільки ж разів більше 4-х, у скількох разів воно буде менше 16. Таке число можна знайти по формулі загального члена геометричної пропорції:
 . Воно і є середньою геометричною для чисел 4 і 16.
. Воно і є середньою геометричною для чисел 4 і 16.
Приклад суперечки Галілея з Наццоліні: кінь коштує 100 крон. Один оцінив її в 1 000, іншої – у 10 крон. Кожна з двох оцінок менш помилкова, чи обидві вони однаково помилкові? Кожний помилився в 10 разів.
Таким чином, якщо середня геометрична 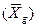 обчислюється з ряду величин (з незгрупованих даних), те вона дорівнює кореню n-ного ступеня з добутку цих величин.
обчислюється з ряду величин (з незгрупованих даних), те вона дорівнює кореню n-ного ступеня з добутку цих величин.
Тобто  ,
,
де  – добуток
– добуток  .
.
Для розрахунку середньої геометричний необхідно значення Х прологарифмувати, тобто
 .
.
У логарифмованому вигляді формула середньої геометричної нагадує формулу середньої арифметичної з тією лише різницею, що замість натуральних величин фігурують їхні логарифми.
У цілому ж середня геометрична відрізняється від середньої арифметичної порядком дій над величинами:
– замість підсумовування величин знаходиться їх добуток;
– замість ділення розраховується корінь відповідного ступеня.
ПРИКЛАД: знайти середню геометричну з 5 чисел:
91, 153, 212, 223, 389.
 .
.
Логарифмуємо:
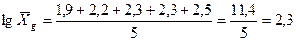 .
.
Звідки  (по таблиці антилогарифмів).
(по таблиці антилогарифмів).
Якщо середня геометрична обчислюється для варіаційного ряду, то тоді сума частот буде показником ступеня кореня, а частота кожного з варіантів – показником ступеня варіанта.
ПРИКЛАД:
| Варіанти (х) | Частоти (f) |
| Разом: |
 .
.
 .
.
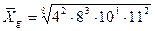 .
.
Середня геометрична має у статистико-економічних дослідженнях дуже обмежене застосування.
Вона використовується, в основному, при розрахунку середніх темпів росту якого-небудь показника (продукції, населення і т.д.).
Середня гармонійна застосовується у випадках, коли осередненню підлягають не самі варіанти, а обернені їм числа  або ж коли є дані про загальний обсяг явища та індивідуальні значення ознаки, але немає відомостей про кількість одиниць даного явища (частотах).
або ж коли є дані про загальний обсяг явища та індивідуальні значення ознаки, але немає відомостей про кількість одиниць даного явища (частотах).
НАПРИКЛАД: є відомості про врожайність і валовий збір зерна, але немає даних про площу зернових (чи є дані про виторг і ціну одиниці товару, але немає кількості реалізованих товарів). Проста середня гармонійна (незважена) визначається:
1. Знаходять середню арифметичну із обернених величин:
 .
.
2. Величина, обернена середній арифметичній і буде середньої гармонійною, тобто:
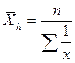 .
.
Слід зазначити, що в теорії статистики немає більш заплутаного і по-різному трактованого питання, чим питання про середню гармонійну.
Багато авторів вважають, що це не самостійний вид середньої, а спосіб скороченого розрахунку середньої арифметичної. Разом з тим, у всіх відомих підручниках середня гармонійна розглядається як різновид середньої і з цим потрібно рахуватися.
Отже, середня гармонійна зважена являє собою не що інше як перетворену середню арифметичну.
Формула для її розрахунку має наступний вигляд:
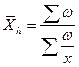 , де
, де 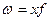 .
.
У багатьох підручниках кочує стандартний приклад розрахунку середньої гармонійної зваженої:
– є середня врожайність зернових у господарствах району  і валовий збір зерна
і валовий збір зерна 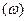 , тобто
, тобто 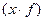 , але немає даних про площу під зернові, тобто немає частоти.
, але немає даних про площу під зернові, тобто немає частоти.
У цьому випадку пропонується обчислювати середню врожайність по району за допомогою середньої гармонійної зваженої.
Хоча, у кінцевому рахунку, її не важко визначити і за допомогою середньої арифметичної розрахувавши попередньо частоту, тобто 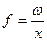 – розділивши валовий збір на врожайність одержимо площу зернових.
– розділивши валовий збір на врожайність одержимо площу зернових.
Середня квадратична застосовується у випадках, коли осередненню (узагальненню) підлягають величини, виражені у вигляді квадратних функцій.
НАПРИКЛАД, середні діаметри труб, коліс, стовбурів дерев і т.д.
Проста середня квадратична визначається за формулою:
 .
.
Зважена:  .
.
Різні види середніх, розраховані на основі однієї і тієї ж первинної інформації мають різну величину:
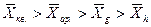 .
.
Читайте також:
- VI. Середня кишка
- VІ Середня хронологічна
- Безпосередня і представницька демократія
- Видаток і середня швидкість ламінарного потоку.
- Геометрична інтерпретація задачі лінійного програмування
- Геометрична інтерпретація задачі нелінійного програмування
- Геометрична інтерпретація ЗЛП. Кононічна форма ЗЛП і її оптимальний план.
- Геометрична інтерпретація розв’язків цілочислових задач лінійного програмування на площині
- Геометрична інтерпретація частинних похідних функції 2-х змінних.
- Геометрична ймовірність
- Геометрична та хвильова оптика.
- Ефективний діаметр молекул. Частота зіткнень та середня довжина вільного пробігу молекул
| <== попередня сторінка | | | наступна сторінка ==> |
| Середня із середніх величин | | | Структурні середні |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |