• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Основні поняття і задачі кореляційного аналізу

Кореляційний аналіз – метод математичної статистики, що вивчає кореляційні (статистичні) зв'язку.

Абстрактно-математичну сторону його більш глибоко і детально розглядають у курсі математичної статистики. Ми ж розглянемо застосування методів кореляційного аналізу у вивченні зв'язків соціально-економічних явищ.

У статистиці розрізняють наступні варіанти кореляційних зв'язків.

1. Парна кореляція, тобто залежність між двома ознаками – результатною і факторною (чи двома факторними).

2. Часткова кореляція – залежність між результатною і однією з факторних ознак при фіксованому значенні інших факторних.

3. Множинна кореляція – залежність між результатною і двома і більш факторними ознаками.

У теорії статистики найбільш розробленою є методологія парної кореляції, оволодіння якою дозволяє пізнати методику вивчення інших варіантів кореляційних зв'язків.

Тому ми і зупинимося тут насамперед на розгляді парної кореляційної залежності.

Необхідно відзначити, що при вивченні кореляційних зв'язків статистика, поряд з кореляційним, використовує і регресійний аналіз. Тому коректніше було б сказати про застосування методів КРА у вивченні кореляційних зв'язків, але для стислості говорять просто – кореляційний аналіз.

Ці два методи вирішують різні задачі, але в цілому служать єдиної меті: вивченню взаємозв'язків соціально-економічних явищ, їх виміру і кількісному вираженню.

Отже, за допомогою методів КРА розв’язуються дві основні задачі.

1. Визначення форми зв'язку і параметрів рівняння зв'язку (це задача регресійного аналізу).

2. Вимір щільності зв'язку (задача кореляційного аналізу).

Перша задача вирішується підбором математичної формули (рівняння зв'язку), що виражає залежність результатної і факторної ознак.

Друга – за допомогою різних показників, що характеризують щільність зв'язку між ознаками (коефіцієнта кореляції, індексу кореляції, кореляційного відношення та ін.).

Схематично КРА можна представити у вигляді таких основних етапів:

1) встановлення наявності зв'язку між досліджуваними ознаками за допомогою зазначених вище методів;

2) вибір найбільш істотних факторів для аналізу;

3) визначення характеру зв'язку, його напрямку і форми, тобто підбір математичного рівняння, що виражає залежність між і ;

4) визначення параметрів рівняння і показників щільності зв'язку;

5) статистична оцінка показників щільності зв'язку.

Найбільш складним і відповідальним етапом КРА є підбір рівняння, що характеризує сутність зв'язку. При парній кореляції рівняння зв'язку може бути встановлене за допомогою побудови кореляційного поля, складання кореляційних таблиць, перегляду різних функцій.

Якщо обсяг досліджуваної сукупності не дуже великий, то доцільно побудувати кореляційне поле, загальний вигляд якого вкаже характер зв'язку, його напрямок і форму.

Тобто, по загальному розташуванню точок кореляційного поля можна установити форму залежності і виразити її відповідним рівнянням:

– лінійна форма рівнянням прямої лінії:

;

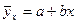– нелінійна форма рівняннями різного роду кривих ліній:

· параболи 2-го 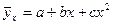порядку чи вищих порядків,

· гіперболи ,

· показової функції й ін.

В економічних явищах і процесах найбільше часто зустрічається лінійна форма зв'язку.

Якщо ж використовуються рівняння нелінійного виду, то застосовують прийом «лінеаризації» функцій, тобто приведення їх до лінійного виду.

Це обумовлено тим, що параметри лінійного рівняння мають гарну економічну інтерпретацію.

Якщо аналіз розташування точок кореляційного поля вказав на лінійну форму зв'язку, то шукане рівняння буде мати вигляд:

,

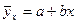де – залежна перемінна (результат);

– незалежна перемінна (фактор);

– параметри прямої лінії, де: – початок відліку чи значення при = 0 ( не має економічного змісту);

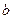– коефіцієнт регресії, що показує середню зміну () при кожній зміні () на одну одиницю.

Коефіцієнт регресії (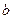) завжди число іменоване.

Якщо: 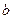> 0, то зв'язок прямий;

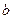< 0, зв'язок обернений;

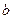= 0 , зв'язок відсутній.

Підібране рівняння називається рівнянням регресії чи кореляційним рівнянням. Його основна задача – установлення кількісного взаємозв'язку між ознаками.

Невідомі параметри рівняння і 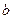визначають способом найменших квадратів із системи нормальних рівнянь.

Суть його в тому, яка на полі кореляції визначається така теоретична лінія регресії, що у порівнянні з безліччю інших ліній, найбільш близько розташована до точок поля (відображає фактичні дані).

Тобто ця лінія дає найменшу суму квадратів відхилень фактичних значень результатної ознаки від вирівняних (теоретичних) значень:

.

Система нормальних рівнянь для парного лінійного зв'язку має вигляд:

,

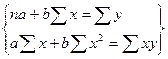де 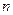– кількість елементів факторної ознаки .

Параметри і 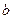шуканої прямої можна визначити і за іншими формулами:

, .

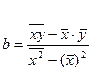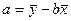Оцінка щільності зв'язку між ознаками передбачає визначення міри відповідності варіації результатної ознаки і факторної (чи декількох факторних при множинній кореляції).

У випадку лінійної залежності щільність зв'язку можна виміряти за допомогою лінійного коефіцієнта кореляції:

,

де 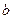– коефіцієнт регресії;

– середнє квадратичне відхилення факторної ознаки;

– середнє квадратичне відхилення результатної ознаки;

; .

Лінійний коефіцієнт кореляції можна визначити і за іншою формулою:

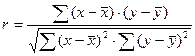або .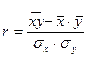

Лінійний коефіцієнт кореляції може приймати значення від 0 до ± 1 (знак (+) при прямої залежності, (-) при оберненій).

На практиці керуються наступними оцінками щільності зв'язку:

При < 0,3 – зв'язок слабкий;

= 0,3 ¸ 0,7 – середній;

> 0,7 – сильний;

= 0 – зв'язок відсутній;

= 1 – зв'язок функціональний.

Значимість ЛКК перевіряється на вірогідність (надійність). Вважається, що кореляційний зв'язок є достовірним лише при достатньому числі спостережень (не менш 20 – 30). Перевірка надійності коефіцієнта кореляції здійснюється за допомогою критерію надійності за формулою:

,

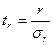де 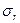– середньоквадратична помилка коефіцієнта кореляції: ,

де 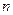– число спостережень.

Якщо ³ 3, то вважається надійним, а зв'язок доведеним з імовірністю 0,997.

Якщо < 3, зв'язок не можна вважати достовірним.

З формули середньої квадратичної помилки видно, що ця помилка знаходиться в зворотній залежності від числа спостережень.

Для всіх інших форм зв'язку щільність її може бути визначена за допомогою теоретичного кореляційного відношення:

,

де 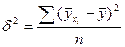– дисперсія вирівняних значень результатної ознаки ();

– дисперсія фактичних значень результатної ознаки ().

Якщо , значить і варіація цілком залежить від варіації .

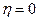Якщо , значить варіація ніяк не впливає на варіацію й у цьому випадку . Тобто, чим ближче до 1, тим зв'язок щільніший, а чим ближче до нуля, тим слабкіший.

Система рівнянь для визначення параметрів рівняння параболи має наступний вигляд:

Читайте також:

1. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
2. II. Поняття соціального процесу.
3. V. Поняття та ознаки (характеристики) злочинності
4. А/. Поняття про судовий процес.
5. Автомати­зовані інформаційні систе­ми для техніч­ного аналізу товар­них, фондових та валют­них ринків.
6. Адвокатура в Україні: основні завдання і функції
7. Адміністративний проступок: поняття, ознаки, види.
8. Адміністративні провадження: поняття, класифікація, стадії
9. Акти застосування юридичних норм: поняття, ознаки, види.
10. Алгоритм однофакторного дисперсійного аналізу за Фішером. Приклад
11. Алгоритм розв’язання задачі
12. Алгоритм розв’язання розподільної задачі

Переглядів: 4744