
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Основні прийоми аналізу рядів динаміки
Складання й аналіз РД здійснюється , як ми уже відзначали, з метою вивчення зміни явищ у часі.
Однією з основних задач, що виникають у процесі аналізу, є встановлення закономірності зміни рівнів (показників) досліджуваного явища.
У деяких випадках закономірність зміни явища, загальна тенденція його розвитку (тренд), цілком чітко виявляється при розгляді рівнів ряду.(Поняття «тренд» введено англійським вченим Гукером у 1902 році).
Так, у наведеному вище прикладі динаміки чисельності населення міста, ясно виявляється тенденція збільшення рівнів.
Однак, на практиці часто доводиться мати справу з рядами, у яких рівні то зростають, то спадають.
У подібних випадках тренд явища простим розглядом ряду не завжди виявляється.
Тому для його виявлення використовуються особливі прийоми обробки РД. Ці прийоми засновані:
– або на перетворенні інтервалів часу й обчисленні середніх рівнів для знову утворених інтервалів;
– або на аналітичному вирівнюванні рівнів РД.
Визначення тренду явища називається вирівнюванням (сгладжуванням) РД, а методи визначення тренду називаються методами вирівнювання.
Вирівнювання дає можливість охарактеризувати особливість зміни в часі даного ДР як функцію часу.
Тобто, воно дозволяє за допомогою часу виразити вплив на явище всіх основних факторів.
Найпростішим прийомом виявлення тренда явища є укрупнення інтервалу (періоду) часу ДР.
Суть його в тому, що первинний РД перетвориться в інший ряд, показники якого відносяться до більш великих інтервалів часу.
НАПРИКЛАД, ряд, що містить дані про місячний випуск продукції перетвориться в ряд квартальних даних і т.д.
При цьому, перетворений ряд може містити як сумарні показники абсолютних величин рівнів первинного ряду, так і середні величини.
Нехай є дані про випуск продукції машинобудівного підприємства за місяцями:
| Місяці | Випуск продукції, млн.грн. | Місяці | Випуск продукції, млн.грн. |
| Січень | 5,1 | Липень | 5,6 |
| Лютий | 5,4 | Серпень | 5,9 |
| Березень | 5,2 | Вересень | 6,1 |
| Квітень | 5,3 | Жовтень | 6,0 |
| Травень | 5,6 | Листопад | 5,9 |
| Червень | 5,8 | Грудень | 6,2 |
Укрупнимо інтервали до 3-х місяців і розрахуємо загальний і середньомісячний випуск продукції за квартали.
| Квартали | Випуск продукції, млн.грн. | Середньомісячний випуск продукції по кварталах, млн.грн. |
| I | 15,7 | 5,23 |
| II | 16,7 | 5,57 |
| III | 17,6 | 5.87 |
| IV | 18,1 | 6,03 |
Отриманий у результаті укрупнення періодів часу ряд більш чітко і наочно відображає загальну закономірність (тенденцію) збільшення випуску продукції.
Тобто при підсумовуванні рівнів і розрахунку середніх за укрупнені інтервали, відхилення в рівнях, обумовлені випадковими причинами, згладжуються. У результаті більш чітко і ясно виявляється дія основних факторів зміни рівнів (загальна тенденція).
Важливим способом виявлення загальної закономірності динамічного ряду є згладжування коливанністі за допомогою ковзної середньої.
Суть його в тому, що фактичні рівні ряду заміняються ковзними (плинними) середніми рівнями, що розраховані для певних укрупнених інтервалів.
Розрахунок ковзної середньої здійснюється таким чином:
1. РД розбивають на певну кількість укрупнених інтервалів, що складаються з однакового числа рівнів. При цьому кожений наступний, після першого, інтервал формують поступово зрушуючи (сковзаючи) на один рівень від початкового. Тобто кожен верхній рівень не включається в знову сформований інтервал. Таким чином, перший інтервал буде містити в собі рівні:
у1 , у2 , … , ym ,
другий у2 , у3 , … , ym+1 ,
третій у3 , у4 , … , ym+2 і т.д.
У результаті інтервал згладжування немов ковзає по ряду зверху вниз із кроком, рівним 1.
2.По кожному зі сформованих інтервалів визначається сума значень рівнів і потім розраховуються ковзні середні як проста середня арифметична.
Розрахована по кожному з інтервалів середня записується напроти центрального рівня даного інтервалу, тобто напроти його серединного рівня.
Обчислення ковзної середньої технічно більш зручне, якщо укрупнені інтервали формувати з непарного числа рівнів (3, 5 наприклад).
Тоді в середині кожного інтервалу виходить один серединний рівень (показник), до якого відноситься розрахована середня.
Розрахунок ковзної середньої за парного числа рівнів створює незручності, тому що в цьому випадку в середині інтервалу виходить 2 серединних рівні і треба знаходити середину між ними (тобто робити процедуру центрування).
Тому на практиці, як правило, завжди намагаються формувати укрупнені інтервали динамічних рядів з непарного числа рівнів.
Порядок розрахунку ковзних середніх розглянемо на прикладі динаміки валового випуску продукції підприємства за 1980-1990 роки.
Як укрупнений інтервал візьмемо 5-річний період часу.
Таблиця показує, що в результаті згладжування коливань рівнів ряду, викликаних різними причинами, у ковзних середніх спостерігається загальна тенденція збільшення випуску продукції.
Тобто тренд даного динамічного ряду має тенденцію зростання. Ефект згладжування, що усуває коливання рівнів і розвитку, що виявляє загальну закономірність розвитку, особливо наочно видно на графіку, що зображує первинний і згладжений за допомогою ковзних середні ряди (рис. 1).
Необхідно відзначити, що метод укрупнення інтервалів і ковзної середньої є найпростішими способами обробки ДР і вони не позбавлені недоліків.
| Роки | Випуск продукції (млн.грн.) | Ковзна сума 5 рівнів | Ковзна середня 5 рівнів |
   1980 1980
| 4,3 | – | – |
  1981 1981
| 4,6 | – | – |
    1982 1982
| 4,3 | 22,0 | 4,4 |
  1983 1983
| 4,5 | 22,9 | 4,6 |
  1984 1984
| 4,3 | 23,6 | 4,7 |
 1985 1985
| 5,2 | 25,0 | 5,0 |
  1986 1986
| 5,3 | 26,5 | 5,3 |
 1987 1987
| 5,7 | 28,2 | 5,6 |
| 6,0 | – | – | |
| 6,0 | – | – |

Рис. 1 Графік первісного і вирівняного рядів
Так, застосування ковзної середньої «укорочує» згладжений ряд, у порівнянні з первинним (фактичним), на число рівнів, рівне (m – 1). Де (m) – число рівнів, що входять в інтервал.
У нашому випадку: 5 – 1 = 4, тобто на 2 рівні з кожного кінця згладженого ряду.
Тому ці прийоми згладжування ДР можна розглядати як важливі допоміжні методи, що полегшують застосування інших, більш досконалих і строгих методів.
Таким більш досконалим способом обробки рядів динаміки з метою встановлення тенденції розвитку (тренду), є вирівнювання ряду за аналітичними формулами, тобто аналітичне вирівнювання.
Суть його полягає в наступному:
– фактичні рівні ряду, що зображені на графіку ламаною лінією, вирівнюються (заміняються) розрахунковими значеннями, отриманими на основі спеціально підібраної математичної формули, що відображує (загальну тенденцію розвитку) тренд даного явища і характеризується деякою плавною лінією: прямою, параболою другого чи іншого порядку, гіперболою, і т.п.
Тобто розраховані рівні розглядаються як функція часу 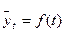 і завдання полягає в тому, щоб підібрати вид (форму) цієї функції.
і завдання полягає в тому, щоб підібрати вид (форму) цієї функції.
Вирівнювання починається з теоретичного аналізу динамічного ряду, у результаті якого встановлюється характер динаміки і тип необхідної лінії.
Найчастіше на практиці доводиться мати справу з вирівнюванням по прямій.
Стосовно до динамічних даних рівняння прямої можна записати у вигляді:
 ,
,
де
 – вирівняні значення рівня ряду;
– вирівняні значення рівня ряду;
t – порядковий номер моменту або періоду часу, до якого відносяться дані;
 – параметри, тобто постійні величини для даної прямої.
– параметри, тобто постійні величини для даної прямої.
Значення t завжди відомі, тому необхідно знайти параметри ( ), що і визначають шукану пряму.
), що і визначають шукану пряму.
Для знаходження параметрів ( ), а отже, і для визначення рівняння вирівняних значень ряду використовується спосіб «найменших квадратів».
), а отже, і для визначення рівняння вирівняних значень ряду використовується спосіб «найменших квадратів».
Суть його в тому, що шукане рівняння прямої повинне бути таким, щоб сума відхилень фактичних рівнів ряду від вирівняних дорівнювало нулю, тобто
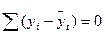 ,
,
а сума квадратів цих відхилень була мінімальною, тобто щоб дотримувалася вимога:
 .
.
Останнє рівняння і відоме як вимога «методу найменших квадратів» (МНК).
Підставляючи в дане рівняння замість  конкретне аналітичне вираження обраної нами для вирівнювання функції, вирішуємо задачу на мінімізацію функції.
конкретне аналітичне вираження обраної нами для вирівнювання функції, вирішуємо задачу на мінімізацію функції.
У нашому випадку при вирівнюванні по прямій  запишемо:
запишемо:
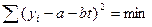 .
.
Щоб визначити при яких значеннях параметрів ( ) ця сума квадратів буде мінімальної, знаходять часткові похідні даної функції по (
) ця сума квадратів буде мінімальної, знаходять часткові похідні даної функції по ( ) і прирівнюють їх до нуля.
) і прирівнюють їх до нуля.
Після нескладних алгебраїчних спрощень одержимо систему нормальних рівнянь, що відповідають вимозі «способу найменших квадратів»:
 ,
,
де y – рівні фактичних значень ряду;
n – кількість рівнів ряду;
t – порядковий номер моменту чи періоду часу.
Розв’язавши цю систему, одержимо параметри ( ) тієї прямої, що ближче усього підходить до ламаній лінії фактичних значень ряду.
) тієї прямої, що ближче усього підходить до ламаній лінії фактичних значень ряду.
Підставивши в рівняння вирівняних значень порядковий номер моменту чи періоду часу, до якого відноситься кожен рівень ряду одержимо вирівняні значення ряду, що відповідають шуканій прямій.
Графічно вирівнювання за «методом найменших квадратів» можна представити таким чином.
Нехай є ряд динаміки випуску продукції:
| Рік | № року | Випуск продукції (млн.грн.) |
| 1-й рік | ||
| 2-й рік | ||
| 3-й рік | ||
| Разом: |
Побудуємо графік динаміки продукції за 3 роки.
 |
с




 30 ¾
30 ¾
 ¾
¾






 20 а в' с’
20 а в' с’
 а'
а'


 10
10
в
 |
1-й рік 2-й рік 3-й рік
Рис. 2 Графік динаміки продукції
 | |||
 | |||



 30 с
30 с



 20 а
20 а

 10 в
10 в
 |
1-й рік 2-й рік 3-й рік
Рис. 3 Можлива безліч прямих
– Між точками а, в, с ламаної лінії графіка динаміки продукції можна провести нескінченну безліч прямих.
– З цієї безлічі прямих (рис. 3) є лише одна, яка з точки зору «методу найменших квадратів» буде найбільш близько підходити до точок (а, в, с) ламаної лінії.
Параметри цієї прямої визначають, як нам уже відомо, із системи нормальних рівнянь, що відповідають вимозі «методу найменших квадратів». Нехай вони становлять: 15, 20, 25.
Таблиця 6.8
Розрахункова таблиця
| Рік (t) | Фактичні значення ряду (yi) | Розрахункові значення (теоретич.)
( ) )
| Відхилення
( ) )
| Квадрати відхилень
( )2 )2
|
| + 5 | ||||
| – 10 | ||||
| + 5 | ||||
| S = 150 = min |
– Якщо знайти цю пряму (нехай це буде пряма а' в' с'), представити її на графіку,
– обчислити відхилення між ординатами (значеннями) точок (а, в, с) ламаної і відповідними значеннями (а' в' с') прямої,
– піднести ці відхилення до квадрату і знайти суму квадратів, то:
отримана сума квадратів відхилень буде менша, ніж кожна з таких сум, обчислених на основі якої-небудь іншої прямої з безлічі прямих, які можна провести між точками (а, в, с) ламаної. Це й ілюструє таблиця 6.8.
Таким чином, знайдена пряма і є тією лінією, що відображує загальну тенденцію випуску продукції за зазначений період часу.
Читайте також:
- II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
- Автоматизовані інформаційні системи для технічного аналізу товарних, фондових та валютних ринків.
- Адвокатура в Україні: основні завдання і функції
- Алгоритм однофакторного дисперсійного аналізу за Фішером. Приклад
- Амортизація основних засобів, основні методи амортизації
- Аналіз динаміки і структури валового нагромадження.
- Аналіз динаміки і структури витрат підприємства
- Аналіз динаміки та структури банківських доходів
- Аналіз динаміки та структури валютних операцій
- Аналіз зображувальних засобів. Застосування цілісного аналізу
- Аналіз рівня, динаміки і структури обсягу виробленої та реалізованої продукції
- Аналіз рівня, динаміки та структури фінансових результатів підприємства
| <== попередня сторінка | | | наступна сторінка ==> |
| Основні поняття і задачі кореляційного аналізу | | | Екстраполяція й інтерполяція |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |