
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
ЗАВДАННЯ ДЛЯ ВИКОНАННЯ ПРАКТИЧНИХ РОБІТ
ПРАКТИЧНА РОБОТА №1
Тема: Аналіз рядів розподілу
Мета практичної роботи:Закріпити на навчальних ситуаціях теоретичний матеріал за темою лекції “Аналіз рядів розподілу”.
Контрольні запитання:
1. Поняття ряду розподілу, його елементи.
2. Види рядів розподілу та методика їх побудови.
3. Характеристики центру розподілу. Мода і медіана в статистиці.
4. Необхідність статистичного вивчення варіації. Основні показники
варіації, їх економічна суть та техніка обчислення.
5. Математичні властивості дисперсії. Правило додавання дисперсій.
6. Характеристики форми розподілу. Коефіцієнти асиметрії та ексцесу.
Практичні заняття з теми передбачають:
1. Варіація ознак. Розмах варіації та середнє лінійне відхилення. Формули. Техніка обчислення. Економічний зміст.
2. Розрахувати дисперсію і середнє квадратичне відхилення. Пояснити техніку обчислення та економічний зміст.
3. Розрахувати коефіцієнт варіації. Пояснити випадки застосування, техніку обчислення та економічний зміст.
4. Обчислення середнього квадратичного відхилення спрощеним способом. Формули і робоча таблиця для розрахунків. Техніка розрахунків.
Методичні вказівки до теми:
Рядом розподілу називається ряд чисел, що характеризує розподіл одиниць досліджуваної сукупності на групи за якоюсь ознакою.
В залежності від того, яка ознака (кількісна чи атрибутивна) покладена в основу ряду розподілу, розрізняють кількісний (варіаційний) та атрибутивний ряди. Варіаційні ряди поділяються на дискретні та інтервальні.
Модою в статистиці називається ознака, що зустрічається в досліджуваній сукупності найчастіше. Для дискретного ряду розподілу модою буде ознака, яка має найбільшу частоту (f).
В інтервальному ряду розподілу мода обчислюється за інтерполяційною формулою:
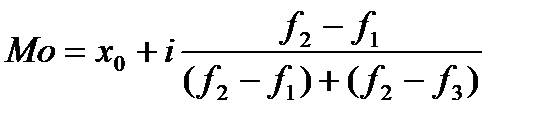 ; (4.1)
; (4.1)
де Мо – мода (конкретне значення);
х0 – нижня межа модального інтервалу;
і - ширина модального інтервалу;
f2 - частота модального інтервалу;
f1 - частота інтервалу, що стоїть перед модальним;
f3 - частота інтервалу, що стоїть після модального.
Медіаною або серединною варіантоюназивається ознака, яка знаходиться в середині ранжированого ряду значень ознаки. Медіана в інтервальному ряду розподілу обчислюється за формулою

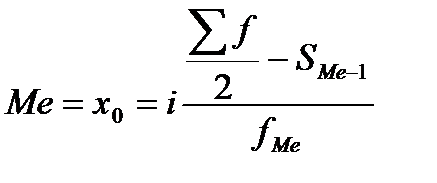 ,(4.2)
,(4.2)
дех0 – нижня межа медіанного інтервалу;
і - ширина медіанного інтервалу;
SMe-1– сума частот, що стоять перед медіанною частотою (кумулятивна частота);
fMe - частота медіанного інтервалу;
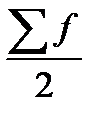 - півсума частот.
- півсума частот.
Варіація - це коливання значень ознаки.
Внаслідок змін у одних сукупностях індивідуальні значення ознаки помітно відхиляються від середнього значення, а в інших — тісно групуються навколо нього.
Міру і ступінь таких відхилень допомагає оцінити ступінь варіації.
Чим менша варіація, тим одно рідніша сукупність, а отже — тим більш надійну характеристику сукупності дають аналітичні середні величини, мода і медіана. І навпаки — чим більша варіація, тим неоднорідніша сукупність.
Для визначення розміру варіації у статистичних розрахунках застосовують такі показники: розмах варіації , середнє лінійне відхилення просте і зважене; середнє квадратичне відхилення просте і зважене;дисперсія проста і зважена ; коефіцієнт варіації.
1.Розмах варіації- це різниця між максимальним і мінімальним значенням ознаки.
R= xmax - xmin,(4.3)
де xmax– найбільше значення ознаки у сукупності;
xmin – найменше значення ознаки у сукупності.
2. Середнє лінійне відхилення (l) обчислюється без урахування знаків (за модулем) за формулами:
ПростеЗважене
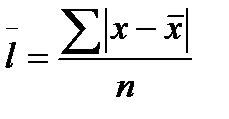 (4.4)
(4.4) 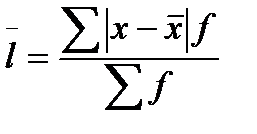 ,(4.5)
,(4.5)
де 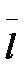 – середнє лінійне відхилення;
– середнє лінійне відхилення;
х – варіанта;
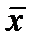 - середнє значення ознаки;
- середнє значення ознаки;
п – число варіант;
f - частота.
3. Середній квадрат відхилення (дисперсія)s2:
ПростаЗважена
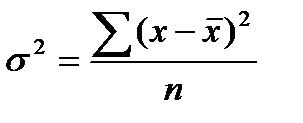 (4.6)
(4.6) 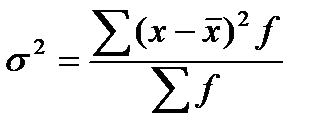 (4.7)
(4.7)
4. Середнє квадратичне відхилення (s):
ПростеЗважене
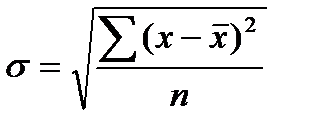 (4.8)
(4.8) 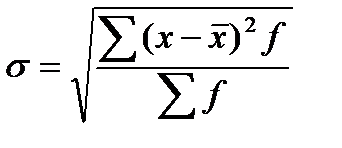 (4.9)
(4.9)
5. Коефіцієнт варіації
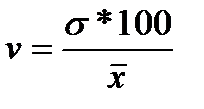 (4.10)
(4.10)
Дисперсія, як і середня арифметична, має властивості, знання яких дозволяє обчислювати середнє квадратичне відхилення спрощеним способом за формулою:  (4.11)
(4.11)
де М1–момент першого порядку, М2 – момент другого порядку. Він дорівнює
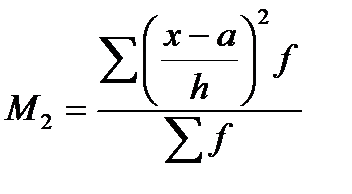 (4.12)
(4.12)
Обчислення зручніше проводити за формулою
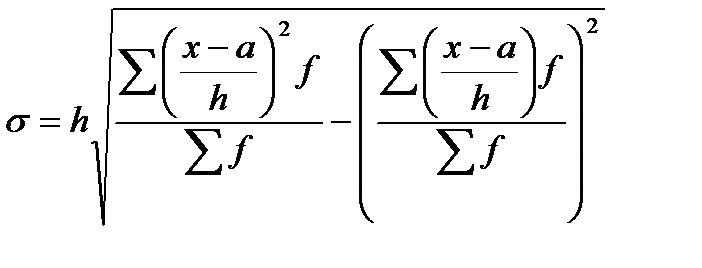 (4.13)
(4.13)
Типові задачі:
1. За даними про розподіл підприємств області за обсягом сплаченого прибуткового податку у розрахунку на одне підприємство визначте:
1) середній обсяг податку, сплаченого одним підприємством області;
2) модальне значення податкових платежів;
3) медіанне значення податкових платежів.
Таблиця 4.1
Розподіл підприємств області за обсягом сплаченого прибуткового податку у розрахунку на одне підприємство
| Обсяг сплаченого прибуткового податку, тис.грн. | До 10 | 10 - 16 | 16 - 22 | 22 - 28 | 28 - 34 | 34 і більше | Разом |
| Кількість підприємств, % |
Розв’язання:
В інтервальному ряді розподілу підприємств за обсягом сплаченого прибуткового податку, припускаючи рівномірний розподіл у межах j-го інтервалу, в якості варіанти 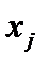 використовують середину інтервалу.
використовують середину інтервалу.
Для розрахунку характеристик центру розподілу складемо розрахункову таблицю.
Таблиця 4.2
Розрахункова таблиця
| Обсяг сплаченого прибуткового податку, тис. грн. | Кількість підприємств, %
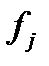
| Середина інтервалу
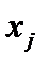
| 
| Кумулятивна (накопичена) частота
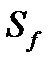
|
| До 10 | ||||
| 10 - 16 | ||||
| 16 - 22 | ||||
| 22 - 28 | ||||
| 22 - 28 | ||||
| 34 і більше | ||||
| Разом | х | х |
1) Середній обсяг прибуткового податку, сплаченого одним підприємством, розраховується за формулою середньої арифметичної зваженої:
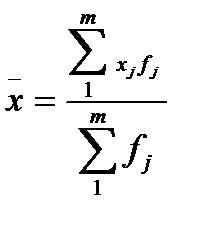 =
= 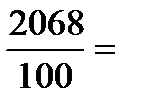 20,7 тис.грн.
20,7 тис.грн.
2) Визначення моди в інтервальному ряду розподілу проводять у два етапи:
- за найбільшою частотою визначають модальний інтервал. За даними таблиці найбільша частота становить 24, отже, модальним є інтервал: 10 – 16;
- у середині модального інтервалу розраховують значення моди за інтерполяційною формулою.
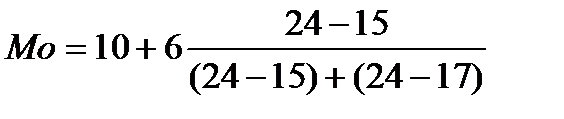 =13,4 тис.грн.
=13,4 тис.грн.
Отже, в області найбільш поширені підприємства з обсягом податкових платежів в інтервалі 10 – 16 тис.грн, а саме 13,4 тис.грн.
3) Визначення медіани за даним рядом розподілу передбачає:
- розрахунок кумулятивних частот;
- визначення медіанного інтервалу за кумулятивною частотою;
- розрахунок значення медіани за інтерполяційною формулою.
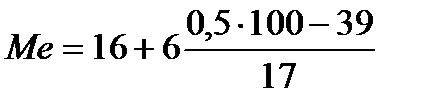 =18,8 тис.грн.
=18,8 тис.грн.
Тобто половина підприємств сплачують прибутковий податок менше 18,8 тис. грн., а друга половина – більше 18,8 тис.грн.
2. Результати торгів на Українській фондовій біржі наведені в таблиці:
Таблиця 4.3
Результати торгів на Українській фондовій біржі
| Вартість угод, млн.грн. | До 40 | 40 - 60 | 60 - 80 | 80 - 100 | 100 і більше | Разом |
| Кількість укладених угод, % |
Визначте:
1) дисперсію;
2) середнє квадратичне відхилення;
3) квадратичний коефіцієнт варіації;
4) дисперсію частки угод вартістю 80 млн.грн. і більше.
Розв’язання:
1)Середня вартість однієї угоди становить: 
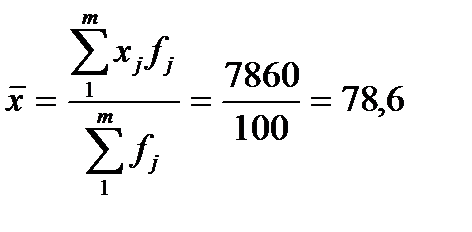 млн.грн., звідси дисперсія
млн.грн., звідси дисперсія 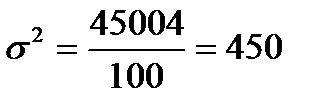 . Порядок розрахунку подано в таблиці:
. Порядок розрахунку подано в таблиці:
Таблиця 4.4
Розрахункова таблиця
| Вартість угод, млн.грн. | Кількість укладених угод, %
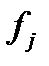
| Середина інтервалу
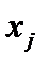
| 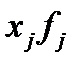
| 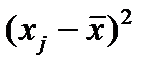
| 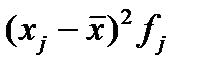
| 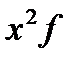
|
| До 40 | 2361,96 | 11809,8 | ||||
| 40 - 60 | 817,96 | 8179,6 | ||||
| 60 - 80 | 73,96 | 3032,4 | ||||
| 80 - 100 | 129,96 | 3249,0 | ||||
| 100 і більше | 985,96 | 18733,3 | ||||
| Разом | х | х |
Дисперсію також можна визначити за формулою різниці квадратів:
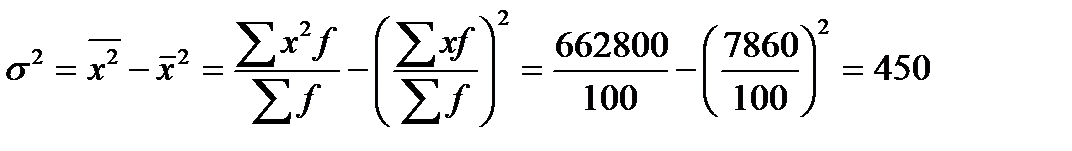 .
.
2)  млн.грн.
млн.грн.
Отже, середнє квадратичне відхилення вартості укладених угод від центра розподілу становить 21,21 млн.грн.
3) 
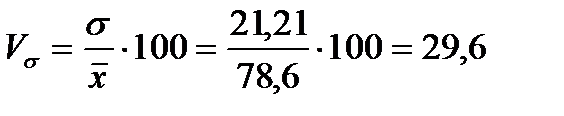 %.
%.
Оскільки 29,6%<33%, то сукупність вважається однорідною, а середня – типовою.
4) Частка угод вартістю 80 млн.грн.і більше становить: 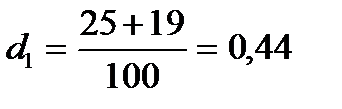
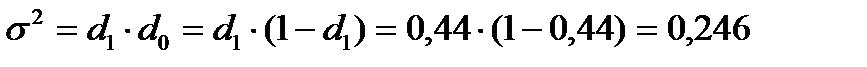 .
.
Завдання для самостійної роботи:
1.Перевіривши дослідні випробування електричних лампочок на тривалість горіння, отримали такі результати:
Таблиця 4.5
Дослідні випробування електричних лампочок на тривалість горіння
| Час горіння, год. | Кількість електроламп |
| До1000 | |
| 1000-2000 | |
| 1200-1400 | |
| 1400-1600 | |
| Понад 1600 | |
| Усього |
Визначити моду та медіану.
2. За результатами опитування сімей про кількість дітей отримали такі дані:
Таблиця 4.6
Розподіл сімей за кількістю дітей
| Кількість дітей | Понад 6 | Усього | ||||||
| Кількість сімей |
Визначити моду і медіану у цьому ряді розподілу.
3. Середньодобовий обсяг виробництва продукції на двох однотипових
підприємствах за місяць однаковий — 140 млн. грн.
Протягом місяця цей показник постійно коливався, і за три декади отримали такі дані, млн. грн.
Таблиця 4.7
Середньодобовий обсяг виробництва продукції
| Декади | |||
| Підприємство №1 | |||
| Підприємство №2 |
Яке підприємство протягом місяця працювало ритмічніше?
4. Розподіл оцінок, отриманих студентами двох груп на екзамені зі статистики характеризується такими даними:
Таблиця 4.8
Розподіл оцінок, отриманих студентами
| Оцінка на екзамені (бал) | Кількість студентів у групах, чол. | |
| група 1 | група 2 | |
| Усього |
У якій групі вищий середній бал і рівномірніша успішність студентів?
5. Маємо вибіркові дані про розподіл населення району за розмірами вкладу в Ощадбанку.
Таблиця 4.9
Розподіл населення району за розмірами вкладу в Ощадбанку
| Розмір вкладу, грн. | До 800 | 800-900 | 900– 1000 | 1000–2000 | Понад 2000 | Усього |
| Число вкладів |
Визначити середній розмір вкладу. для обчислення зміни варіації вкладу використайте середнє квадратичне відхилення і коефіцієнт варіації.
Поясніть економічний зміст цих показників.
6. Опитуванням 100 українських жінок про час, затрачений на домашню роботу, отримали такі дані:
Таблиця 4.10
Розподіл часу затраченого на домашню роботу
| Кількість годин | До1 | 1-2 | 2-3 | 3-4 | 4-5 | 5-6 | Усього |
| Число жінок |
Обчислити середні затрати часу на домашню роботу та показники варіації, які би показали коливання цієї цифри.
7. Маємо такі дані про обсяг роздрібного товарообігу на одного продавця:
Таблиця 4.11
Обсяг роздрібного товарообігу на одного продавця
| Товарообіг, тис. грн. | Середня облікова кількість працівників | |
| В минулому році | В звітному році | |
| До 3 | ||
| 3-4 | ||
| 4-6 | ||
| 6 та більше |
Обчислити способом моментів середній виробіток одного працівника у минулому та звітному роках. Обчислити показники варіації і зробити висновки.
Література: основна [1-3, 7, 8]
додаткова [ 5, 8, 9]
| <== попередня сторінка | | | наступна сторінка ==> |
| Приклади розв’язку задач | | | ПРАКТИЧНА РОБОТА № 2 |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |