
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Геометричній зміст похідної
Розглянемо графік функції 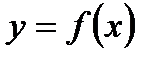 і точку
і точку 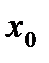 , яка є внутрішньою точкою області визначення. Зокрема, це означає, що функція визначена в деякому околі
, яка є внутрішньою точкою області визначення. Зокрема, це означає, що функція визначена в деякому околі 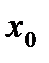 .
.
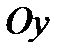
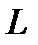
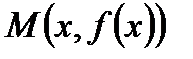
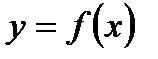
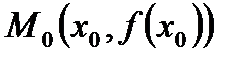
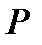
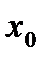
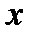
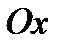
Точці 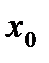 на графіку відповідає точка
на графіку відповідає точка 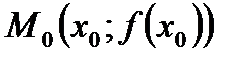 . Проведемо через точку
. Проведемо через точку 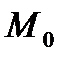 січну, яка перетинає графік у поточній точці
січну, яка перетинає графік у поточній точці 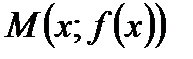 . Позначимо
. Позначимо 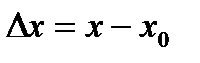 . Різницю значень функції в цих точках позначимо:
. Різницю значень функції в цих точках позначимо:
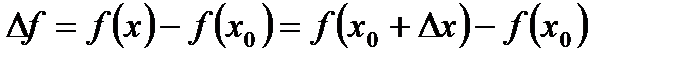 .
.
Січна утворює з віссю абсцис кут, який дорівнює куту 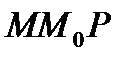 . Тангенс цього кута дорівнює
. Тангенс цього кута дорівнює 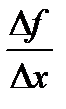 і залежить від положення точки
і залежить від положення точки 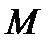 . Будемо пересувати точку
. Будемо пересувати точку 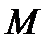 до точки
до точки 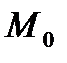 . При цьому січна буде повертатися навколо точки
. При цьому січна буде повертатися навколо точки 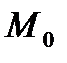 , а дуга
, а дуга 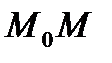 прямуватиме до нуля.
прямуватиме до нуля.
Означення 4.4. Дотичною до графіка функції 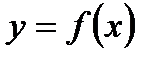 у точці
у точці 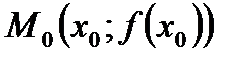 називається граничне положення січної
називається граничне положення січної 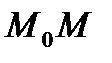 , яке вона займає, при тому що дуга
, яке вона займає, при тому що дуга 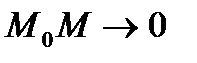 .
.
Кут нахилу дотичної 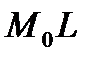 ,
, 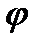 буде знаходитися як границя кутів
буде знаходитися як границя кутів 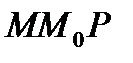 , при
, при 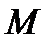 , що прямує до
, що прямує до 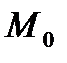 , тобто
, тобто 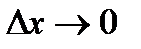 . Як відомо, кутовий коефіцієнт існує не у всіх прямих. Якщо
. Як відомо, кутовий коефіцієнт існує не у всіх прямих. Якщо 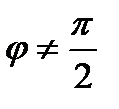 , то кутовий коефіцієнт дотичної буде дорівнювати:
, то кутовий коефіцієнт дотичної буде дорівнювати:
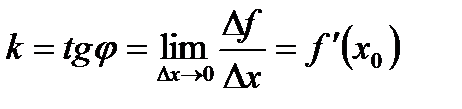 .
.
Отже, для випадку, коли дотична не перпендикулярна вісі абсцис, похідна функції в точці дорівнює кутовому коефіцієнту дотичної. Якщо ж дотична перпендикулярна до вісі абсцис, то похідна не існує, 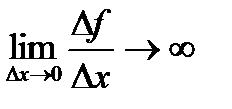 .
.
Таким чином, між похідною та дотичною існує такий зв'язок: якщо існує похідна в точці, то до графіка функції у відповідній точці існує дотична, але якщо в точці існує дотична, то похідна в цій точці може не існувати.
Приклад. Розглянемо поведінку функції 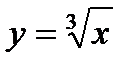 в точці
в точці 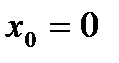 . Дотична в цій точці існує і перпендикулярна до вісі абсцис, а похідна,
. Дотична в цій точці існує і перпендикулярна до вісі абсцис, а похідна, 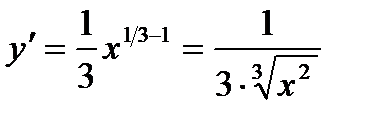 , не існує.
, не існує.
Зауваження. Нехай функція визначена на відрізку 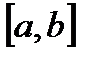 . За означенням, похідна функції в точці є границею, а необхідною і достатньою умовою існування границі є існування та рівність односторонніх границь. Оскільки функція не визначена зліва від точки
. За означенням, похідна функції в точці є границею, а необхідною і достатньою умовою існування границі є існування та рівність односторонніх границь. Оскільки функція не визначена зліва від точки 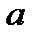 , то лівостороння границя тут не існує, отже, не існує границя взагалі, тобто похідна також не існує. Аналогічна ситуація в точці
, то лівостороння границя тут не існує, отже, не існує границя взагалі, тобто похідна також не існує. Аналогічна ситуація в точці 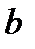 . Таким чином, якщо функція визначена на відрізку
. Таким чином, якщо функція визначена на відрізку 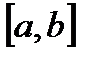 , то вона може мати похідну лише на інтервалі
, то вона може мати похідну лише на інтервалі 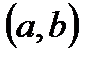 .
.
Теорема 4.1. (Зв'язок між похідною і неперервністю). Якщо існує похідна функції в точці  , то функція неперервна у
, то функція неперервна у  .
.
Доведення Якщо в точці  існує похідна, то з означення похідної функції в точці та означення границі функції випливає, що прирощення функції можна подати у вигляді:
існує похідна, то з означення похідної функції в точці та означення границі функції випливає, що прирощення функції можна подати у вигляді:
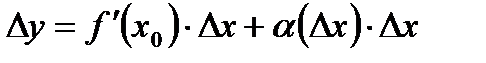 ,
,
де 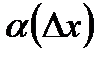 - нескінченно мала величина при
- нескінченно мала величина при 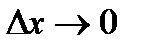 .
.
Таким чином, нескінченно малому прирощенню аргументу відповідає нескінченно мале прирощення функції, а це, за одним з означень неперервності, установлює неперервність функції в точці  .
.
Зауважимо, що обернене твердження не є істинним. Прикладом є функція 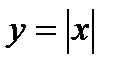 . У точці
. У точці 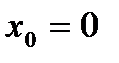 функція є неперервною, але похідна тут не існує. Дійсно, ця функція не є елементарною, оскільки визначається двома різними аналітичними виразами:
функція є неперервною, але похідна тут не існує. Дійсно, ця функція не є елементарною, оскільки визначається двома різними аналітичними виразами: 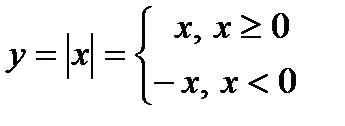 . У точці
. У точці 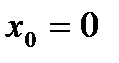 ця функція неперервна: границя функції при
ця функція неперервна: границя функції при 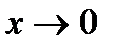 існує:
існує: 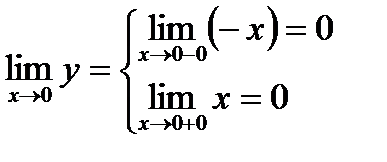 . Обидві односторонні границі існують і є рівними, отже,
. Обидві односторонні границі існують і є рівними, отже, 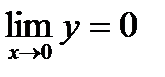 і дорівнює значенню функції в точці
і дорівнює значенню функції в точці 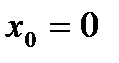 . У той же час похідна в цій точці не існує. Дійсно, будемо шукати похідну. Прирощення аргументу в точці
. У той же час похідна в цій точці не існує. Дійсно, будемо шукати похідну. Прирощення аргументу в точці 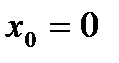 дорівнює:
дорівнює: 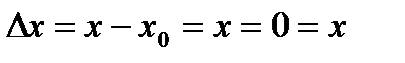 , прирощення функції
, прирощення функції 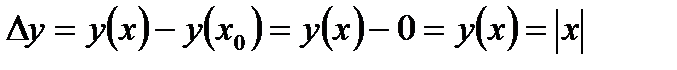 і становитиме
і становитиме 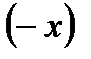 при
при 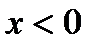 та
та 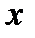 при
при 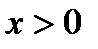 . Таким чином, лівостороння границя відношення прирощень,
. Таким чином, лівостороння границя відношення прирощень, 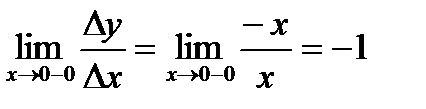 , а правостороння
, а правостороння 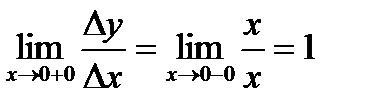 і вони не рівні, отже, границя не існує, тобто в цій точці похідна не існує. Це можна побачити на графіку функції:
і вони не рівні, отже, границя не існує, тобто в цій точці похідна не існує. Це можна побачити на графіку функції:
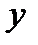
|
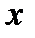
|
|
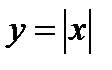
|
Усі січні, які будуються зліва від 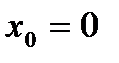 , співпадають з графіком функції
, співпадають з графіком функції 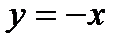 , а справа з графіком
, а справа з графіком 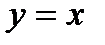 , тобто граничного положення січних не існує.
, тобто граничного положення січних не існує.
| <== попередня сторінка | | | наступна сторінка ==> |
| Диференціальне числення | | | Арифметичні теореми про похідну |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |