
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Арифметичні теореми про похідну
Теорема 4.2. Якщо функції 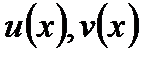 мають похідні в точці
мають похідні в точці  , то існує похідна суми цих функцій, яка дорівнює сумі похідних:
, то існує похідна суми цих функцій, яка дорівнює сумі похідних:
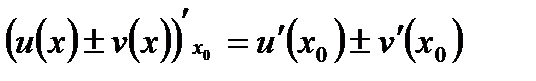 .
.
Доведення. Розглянемо функцію 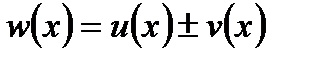 .
.
Знайдемо прирощення цієї функції в точці  :
: 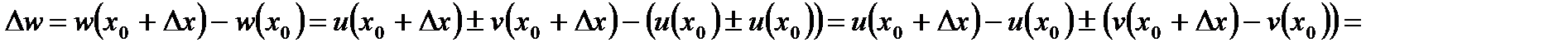
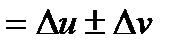 . За означенням похідної:
. За означенням похідної:
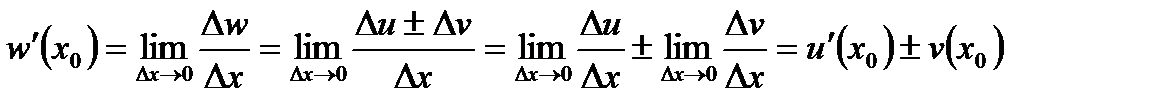 .
.
Теорема 4.3. Якщо функції 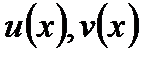 мають похідні в точці
мають похідні в точці  , то існує похідна їх добутку, яка дорівнює сумі добутків похідної першої функції на другу та похідній другої функції на першу:
, то існує похідна їх добутку, яка дорівнює сумі добутків похідної першої функції на другу та похідній другої функції на першу:
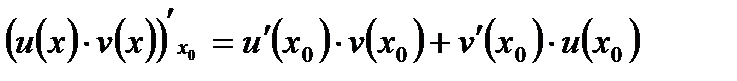 .
.
Доведення. Розглянемо функцію 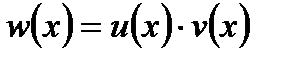 . Знайдемо прирощення цієї функції в точці
. Знайдемо прирощення цієї функції в точці  :
: 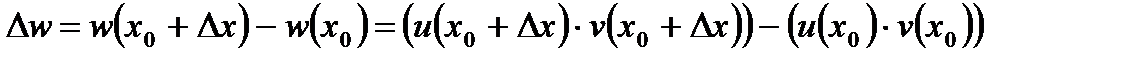 . Додамо і віднімемо вираз
. Додамо і віднімемо вираз 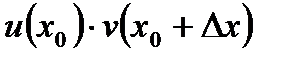 , отримаємо:
, отримаємо: 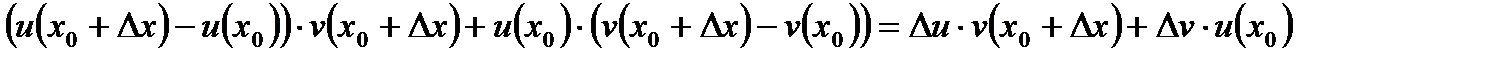 . За означенням похідної:
. За означенням похідної:
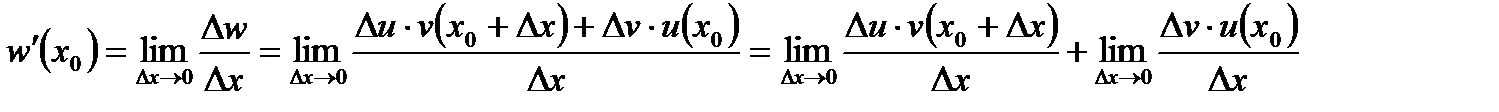 .
.
Функція 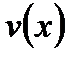 має похідну в точці
має похідну в точці  , отже, вона неперервна в цій точці, тому
, отже, вона неперервна в цій точці, тому 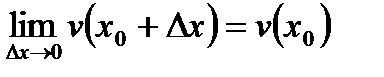 . Функція
. Функція 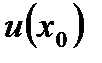 є сталою при
є сталою при 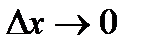 , отже,
, отже,
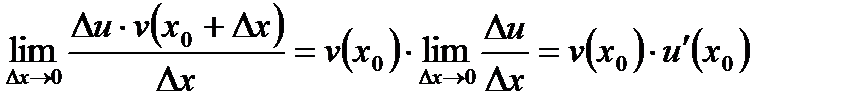 .
.
Аналогічно, другий доданок дорівнює 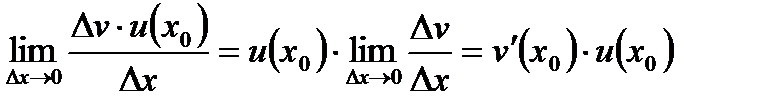 . Остаточно, отримаємо:
. Остаточно, отримаємо: 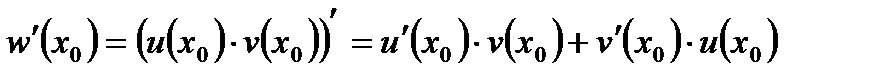
Теорема 4.4. Похідна сталої величини дорівнює нулю:
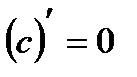 .
.
Доведення. Розглянемо функцію 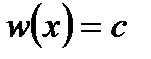 . Її прирощення
. Її прирощення 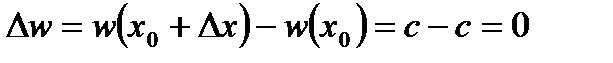 . Тоді:
. Тоді:
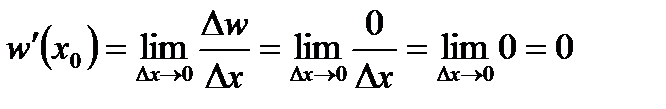 .
.
Наслідок з теорем 4.3. та 4.4: Сталу величину можна виносити за знак похідної:
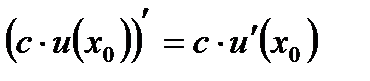 .
.
Теорема 4.5. Якщо функції 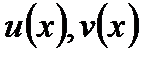 мають похідні в точці
мають похідні в точці  і функція
і функція 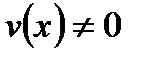 в деякому околі точки
в деякому околі точки  , то в цій точці існує похідна частки
, то в цій точці існує похідна частки 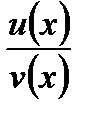 , яка дорівнює:
, яка дорівнює:
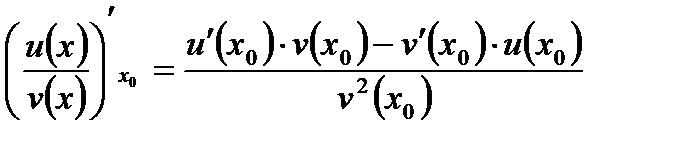 .
.
Доведення. Розглянемо функцію 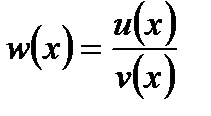 . Прирощення цієї функції дорівнює:
. Прирощення цієї функції дорівнює: 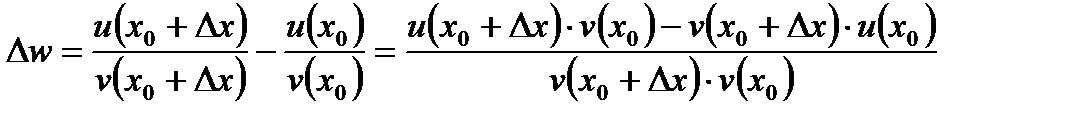 . Віднімемо і додамо в чисельнику вираз
. Віднімемо і додамо в чисельнику вираз  , отримаємо:
, отримаємо: 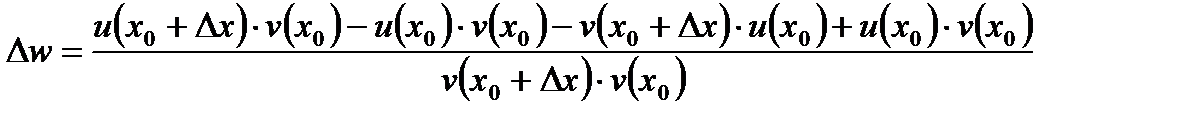 ,
,
Або 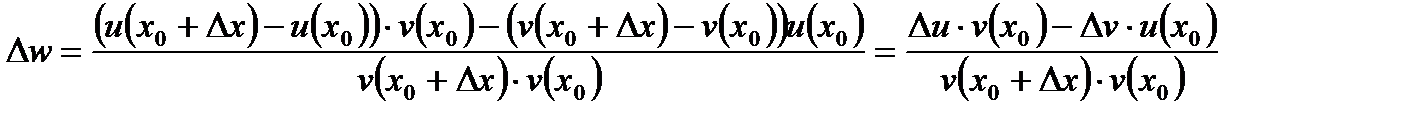 . Границя відношення буде така:
. Границя відношення буде така: 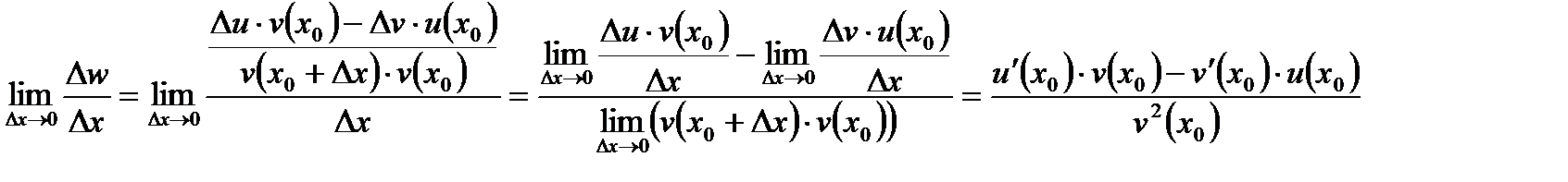 .
.
Теорема 4.6. Якщо функція 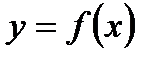 строго монотонна в деякому околі точки
строго монотонна в деякому околі точки 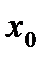 і має в тій точці похідну, яка не дорівнює нулю, то існує обернена їй функція
і має в тій точці похідну, яка не дорівнює нулю, то існує обернена їй функція 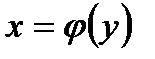 , яка визначена в деякому околі точки
, яка визначена в деякому околі точки 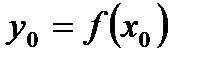 та її похідна дорівнює:
та її похідна дорівнює:
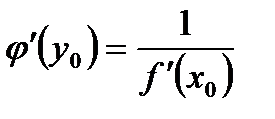 .
.
Теорема 4.7. Якщо функція 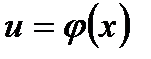 має похідну в точці
має похідну в точці 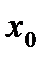 :
: 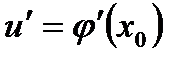 , а функція
, а функція 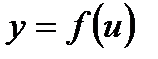 має похідну в точці
має похідну в точці 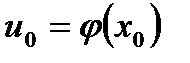 :
: 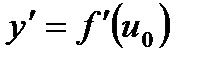 , то складена функція
, то складена функція 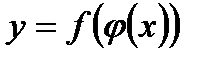 має похідну в точці
має похідну в точці 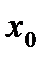 , яка дорівнює:
, яка дорівнює:
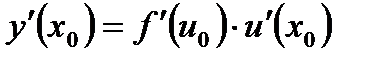 .
.
Вище були знайдені похідні сталої та функції 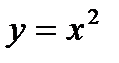 . Доведемо формули обчислення похідних ще декількох елементарних функцій.
. Доведемо формули обчислення похідних ще декількох елементарних функцій.
1. Логарифмічна функція: 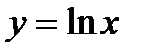 . Розглянемо довільну точку
. Розглянемо довільну точку 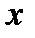 , яка належить області визначення функції. Задамо пророщення аргументу
, яка належить області визначення функції. Задамо пророщення аргументу 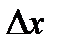 таке, що точка
таке, що точка 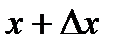 також належить області визначення. Прирощення функції має вигляд:
також належить області визначення. Прирощення функції має вигляд: 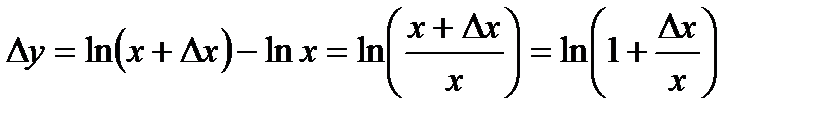 . Тоді похідна в цій точці буде дорівнювати:
. Тоді похідна в цій точці буде дорівнювати: 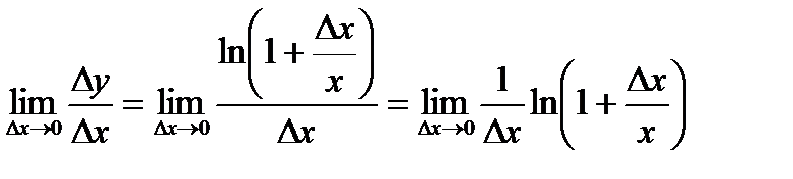 . Помножимо і поділимо дріб на
. Помножимо і поділимо дріб на 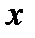 та скористаємося властивостями логарифма:
та скористаємося властивостями логарифма:
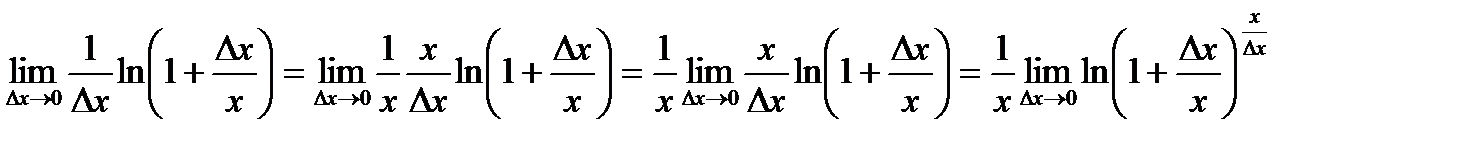 .
.
У процесі 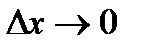 , величина
, величина 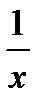 є сталою і її можна винести за знак границі. Функція
є сталою і її можна винести за знак границі. Функція 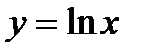 неперервна, отже, символи функції та границі комутативні, тому:
неперервна, отже, символи функції та границі комутативні, тому: 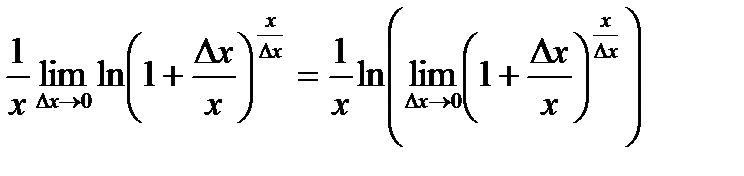 .
.
Границя, яку нам треба обчислити, 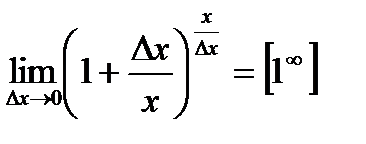 - друга важлива границя, отже,
- друга важлива границя, отже, 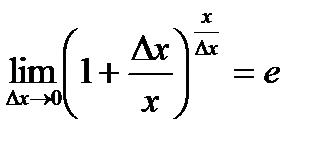 . Остаточно, отримаємо:
. Остаточно, отримаємо:
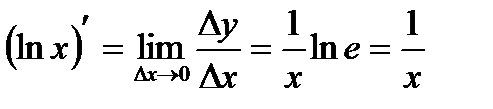 .
.
Тепер можна знайти похідну функції 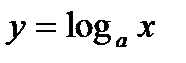 :
:
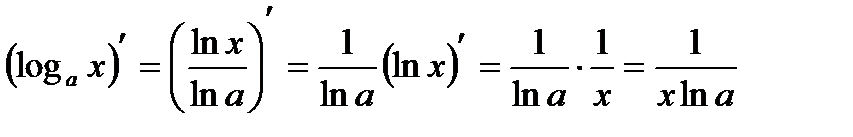 .
.
2. Показникова функція: 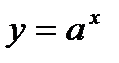 . Прологарифмуємо обидві частини:
. Прологарифмуємо обидві частини: 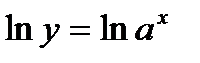 , або
, або 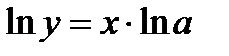 , та знайдемо похідні лівої та правої частини, ураховуючи, що в лівій частині складена функція:
, та знайдемо похідні лівої та правої частини, ураховуючи, що в лівій частині складена функція: 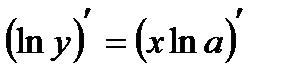 , або
, або 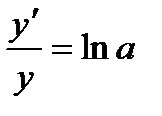 . Звідси:
. Звідси:  , або
, або 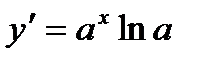 .
.
3. Степенева функція 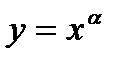 . Прологарифмуємо обидві частини:
. Прологарифмуємо обидві частини: 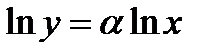 та знайдемо похідні лівої та правої частин, ураховуючи, що в лівій частині складена функція:
та знайдемо похідні лівої та правої частин, ураховуючи, що в лівій частині складена функція: 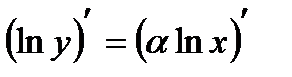 , або
, або 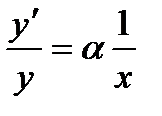 . Звідси:
. Звідси: 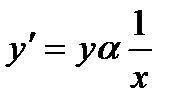 , або
, або 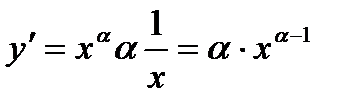 .
.
4. Тригонометричні функції: 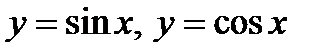 . Знайдемо прирощення функції
. Знайдемо прирощення функції 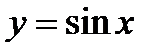 :
:
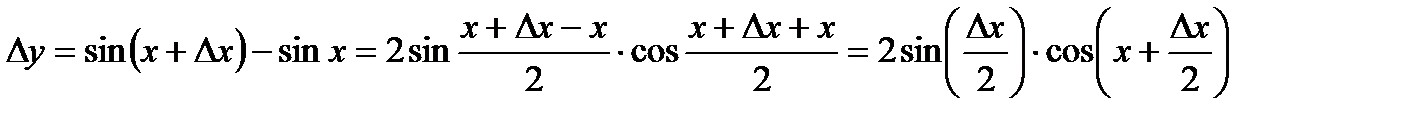 та обчислимо границю відношення
та обчислимо границю відношення
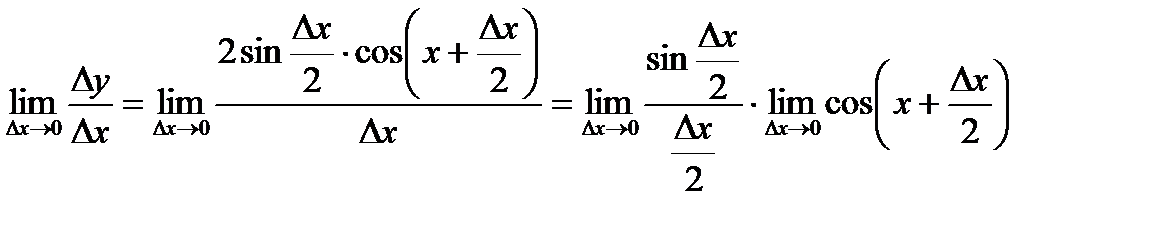 .
.
Перший співмножник – перша важлива границя, яка дорівнює одиниці, а другий – границя неперервної функції, отже, вона дорівнює значенню функції в точці. Таким чином, 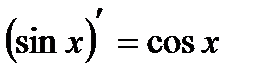 .
.
Для знаходження похідної функції 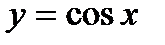 , скористаємося формулами зведення, за якими
, скористаємося формулами зведення, за якими 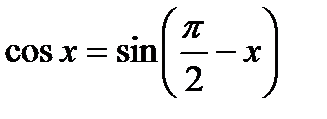 . Маємо:
. Маємо:
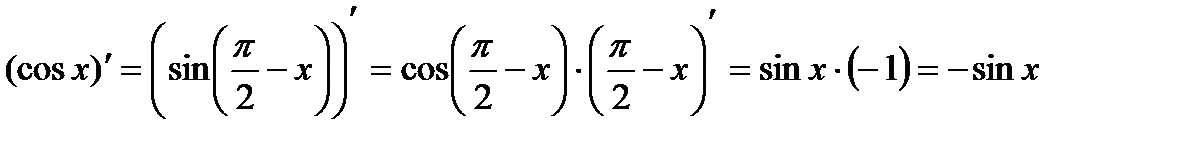 .
.
Похідні функцій 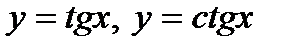 легко знайти, згадавши, що
легко знайти, згадавши, що 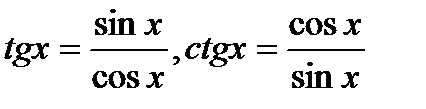 , і скориставшись формулою похідної дробу.
, і скориставшись формулою похідної дробу.
Наведемо формулювання ще двох теорем.
Теорема 4.8. (Теорема Лагранжа). Якщо функція 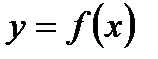 визначена на відрізку
визначена на відрізку 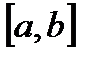 і має похідну в інтервалі
і має похідну в інтервалі 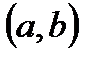 , то існує точка
, то існує точка 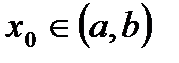 така, що
така, що
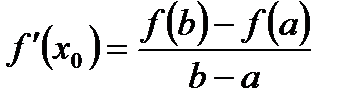 .
.
Геометрична ілюстрація теореми. Якщо з’єднати точки 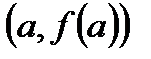 та
та 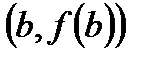 відрізком, то існує точка
відрізком, то існує точка 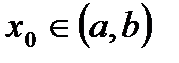 , дотична в якій паралельна цьому відрізку.
, дотична в якій паралельна цьому відрізку.
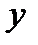
|
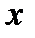
|
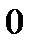
|
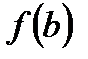
|
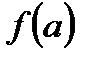
|
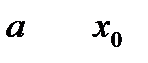
|
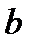
|
Теорема 4.8. (Правило Лопіталя). Якщо при 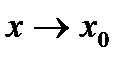 або
або 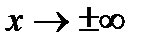 функції
функції 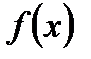 та
та 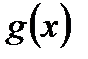 одночасно є нескінченно великими, або нескінченно малими, то границя відношення їх частки дорівнює границі відношення їх похідних:
одночасно є нескінченно великими, або нескінченно малими, то границя відношення їх частки дорівнює границі відношення їх похідних:
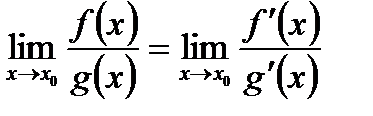 і
і 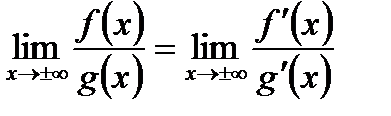 .
.
Ця теорема застосовується при розкритті деяких невизначеностей.
Приклад.
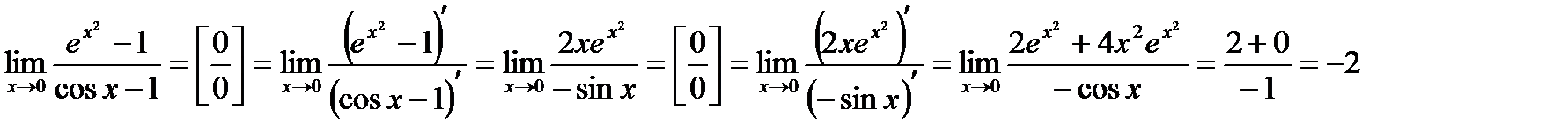
Таблиця похідних елементарних функцій
(В усіх формулах вважається, що функції є складеними, причому внутрішня функція 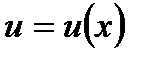 має похідну в кожній точці деякого числового проміжку).
має похідну в кожній точці деякого числового проміжку).
1. 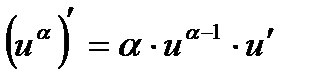
| 6. 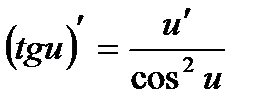
|
2. 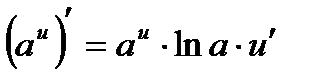
| 7. 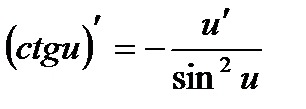
|
2а. 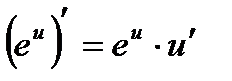
| 8. 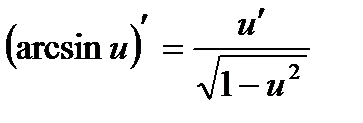
|
3. 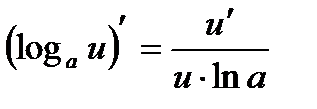
| 9. 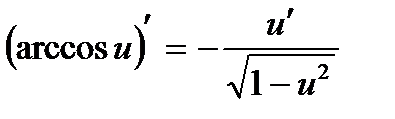
|
3а. 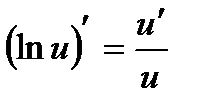
| 10. 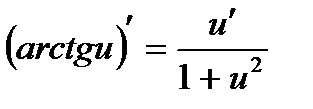
|
4. 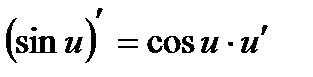
| 11. 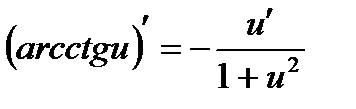
|
5. 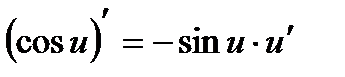
|

Приклад. Знайти похідну функції: 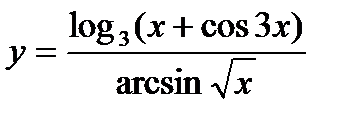 .
.
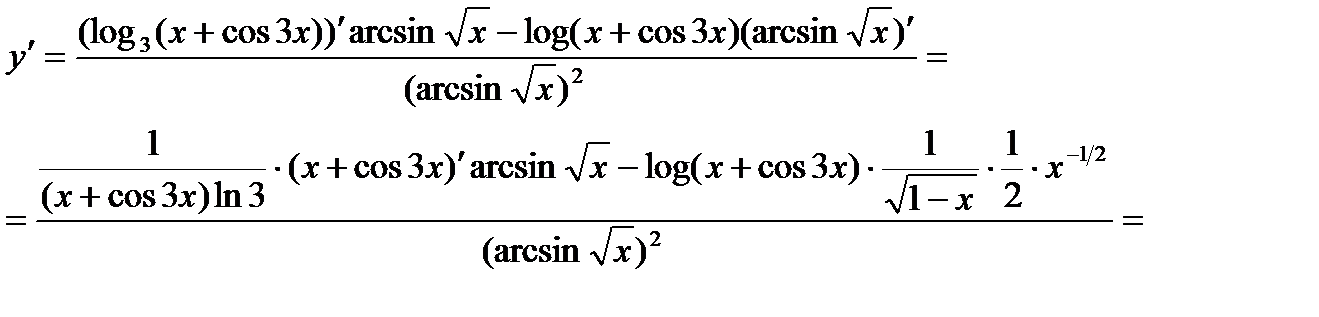
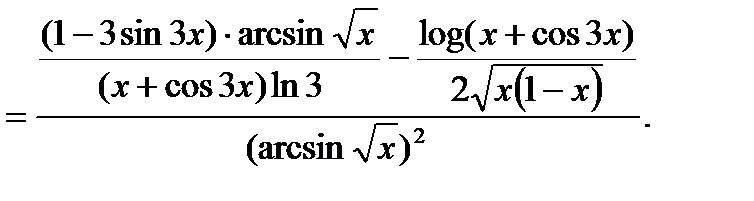
| <== попередня сторінка | | | наступна сторінка ==> |
| Геометричній зміст похідної | | | Похідні вищих порядків |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |