• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Опорний конспект лекцій

з дисципліни Вища математика

для студентів заочної, прискореної форми навчання (ТСМ, ІМЗ)

(III курс, II семестр), лекція 6

Розділ 7. Теорія ймовірності та математична статистика

Доцент к.ф.т.н. Плешівський Я.М.

Львів

2014р.

Основні поняття комбінаторики.

Комбінаторика – це розділ математики, в якому розглядають різні комбінації скінченної кількості елементів та обчислюють число усіх можливих таких комбінацій.

До основних понять комбінаторики належать поняття розміщення, комбінації (сполуки) та перестановки.

Перестановкоюn елементів називають властивий в скінченій n- елементів множині порядок. Число всіх можливих перестановок з n елементів позначають 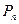і обчислюють за формулою

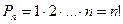
Розміщення . Множина, в якій задано порядок розміщення її елементів називається впорядкованою. Розглянемо скінчену множину з n елементів.усяка її впорядкована m- елементів множина ( 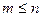) називається розміщенням з n елементів по m. Число всіх можливих m- елементних розміщень для множини з n елементів (число всіх можливих розміщень з n по m) обчислюється за формулою:

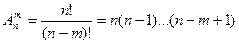
Вважють, що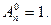

Комбінацією (сполукою) називають m- елементну підмножину n-елементної множини, або просто підмножину з n елементів по m.

Підмножини, які відрізняються одна від одної порядком розміщення елементів, не вважають різними.

Число всіх можливих підмножин по m елементів в кожній, для множини з n елементів, тобто число сполучень з n елементів по m елементів в кожному, позначають 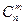і обчислюють за формулою:

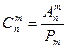або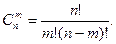

Число сполучень має такі властивості:

.

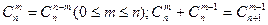Наприклад:

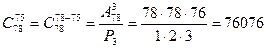
Приклад 1. Перед випуском група учнів з 30 чоловік обмінялися фотокартками. Скільки всього було роздано фотокарток?

Розв’язання: Предавання фотокарток одним учнем другому є розміщення з 30 елементів по два елементи. Шукане число фотокарток рівне числу розміщення з 30 елементів по два елементи в кожному:

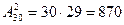
Приклад 2. Скільки чотиризначних чисел можна скласти з цифр 1,2,3,4 без повторень?

Розв’язання: По умові дано множину з чотирьох елементів, які потрібно розташувати в певній послідовності. Значить,потрібно знайти кількість перестановок з чотирьох елементів:

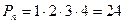
Тобто з цифр 1,2,3,4 можна скласти 24 чотиризначних числа (без повторень цифр).

Приклад 3. Скількома способами можна розмістити 10 гостей на десяти місцях за святковим столом?

Розв’язання: Шукане число способів дорівнює числу перестановок із десяти елементів:

.

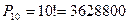Приклад 4. Скільки всього ігор мають провести 20 футбольних команд в одному чемпіонаті?

Розв’язання: Тому, що гра будь-якої команди А з командою В співпадає з грою команди В з командою А, то кожна гра є сполученням з 20 елементів по 2. шукане число усіх ігор дорівнює числу сполучень з 20 елементів по 2 елементи в кожному:

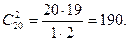
Приклад 5. Скількома способами можна розподілити 12 чоловік по бригадах, якщо в кожній бригаді 6 чоловік?

Розв’язок: склад кожної бригади є 6-елементною підмножиною множини з 12 елементів. Значить, шукане число способів дорівнює числу сполучень з 12 елементів по 6 в кожному:

Переглядів: 1060