
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Випадкові події. Ймовірність події.
Теорія ймовірності вивчає закономірності у випадкових подіях. Основними поняттями теорії ймовірності є випробування і події.
Під випробуванням (дослідом) розуміють реалізацію комплексу умов, внаслідок якого неодмінно відбудеться яка-небудь подія.
Наприклад: кидання монети - випробування; поява герба чи цифри - події.
Випадковою подією називають подію, пов’язану з даними випробуваннями, яка при здійснені випробування може відбутися, а може і не відбутися. Слово “випадкова” для стислості часто опускають і говорять просто подія. Наприклад, постріл по цілі – це дослід, випадкової події у цьому досліді – попадання в ціль або промах.
Подія називається вірогідною, якщо в результаті досліду вона обов’язково відбудеться і неможливою, якщо вона не може відбутися. Наприклад: випадання не більше шести очок при киданні однієї гральної кості – вірогідна подія; випадання десяти очок при киданні однієї гральної кості – неможлива подія.
Події називаються несумісними, якщо ніякі дві з них не можуть відбутися одночасно.
Наприклад: попадання і промах при одному пострілі – це несумісні події.
Говорять, що декілька подій у даному досліді утворюють повну системуподій, якщо в результаті досліду неодмінно повинно відбутися хоча б одна з них. Наприклад: при киданні гральної кості події, які полягають у випаданні одного, двох, трьох, чотирьох, п’яти і шести очок, утворюють повну систему подій.
Події називають рівно можливими, якщо ні одна з них не є об’єктивно більш можлива, ніж інша. Наприклад при киданні монети випадання герба чи числа – події рівно можливі.
Кожна подія має якусь степінь можливості. Числова міра степеня об’єктивної можливості події – це ймовірність події.
Ймовірність події А позначається Р(А).
Нехай з системи n - несумісних рівно можливих наслідків випробувань m – наслідків сприяють події А. Тоді ймовірність події А обчислюється по формулі:
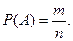
Ця формула носить назву класичного означення ймовірності.
Якщо В – вірогідна подія, то m=n, отже Р(В)=1;
Якщо С – неможлива подія, то m=0, отже Р(С)=0;
Якщо А – випадкова подія, то 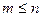 , отже Р(А)
, отже Р(А) 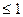 ;
;
Тому ймовірність події знаходиться в межах
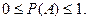
Розглянемо приклади безпосереднього обчислення ймовірності.
Приклад 6. Гральну кістку кидають один раз.
Знайти ймовірність події: А – появи парного числа очок; В – появи не менше п’яти очок; С – появи не більше п’яти очок.
Розв’язання: дослід має шість рівно можливих незалежних наслідків (поява одного, двох, трьох, чотирьох, п’яти і шести очок), які утворюють повну систему.
Події А сприяють три наслідки (випадання двох, трьох, чотирьох і шести очок) тому Р(А)=3/6=1/2; події В – два наслідки (випадання п’яти і шести очок) тому Р(В)=2/6=1/3; події С – п’яти наслідків (випадання п’яти, одного, двох, трьох, чотирьох очок), тому Р(С)=5/6.
При обчисленні ймовірності події часто доводиться використовувати формули комбінаторики.
Приклад 7. В урні знаходиться 7 червоних і 6 синіх кульок. З урни одночасно виймають дві кулі. Знайдіть ймовірність того, що обидві кулі червоні (подія А).
Розв’язання: Число рівно можливих незалежних наслідків дорівнює:
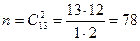
Події А сприяють 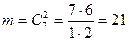 наслідків.
наслідків.
Отже, Р(А)= 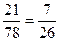 .
.
Приклад 8. В партії з 24 деталей п’ять бракованих. З партії вибирають навмання 6 деталей. Знайдіть ймовірність того, що серед цих 6 деталей виявиться 2 браковані (подія В).
Розв’язання: Число рівно можливих незалежних подій дорівнює
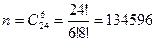
Підраховуємо число наслідків, сприятливих для події В. серед 6 взятих навмання деталей повинно бути 2 браковані і 4 стандартні. Дві браковані деталі з п’яти можна вибрати 
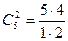 способами, а 4 стандартних деталі з 19 стандартних деталей можна вибрати
способами, а 4 стандартних деталі з 19 стандартних деталей можна вибрати 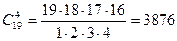 способами.
способами.
Кожна комбінація бракованих деталей може сполучатися з кожною комбінацією стандартних деталей, тому
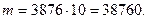
Отже,
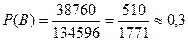
Приклад 9. Дев’ять різних книг розташовані навмання на одній полиці. Знайти ймовірність того, що книжки виявляються поставленими поряд (подія С).
Розв’язання: Тут число рівно можливих незалежних наслідків є 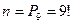 Уявимо собі, що чотири певних книг пов’язані разом, тоді цю зв’язку можна розташувати на полиці
Уявимо собі, що чотири певних книг пов’язані разом, тоді цю зв’язку можна розташувати на полиці  способоми (зв’язку додати до решти п’яти книг). В середині зв’язки чотири можна переставити
способоми (зв’язку додати до решти п’яти книг). В середині зв’язки чотири можна переставити 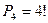 способами. При цьому кожна комбінація в середині зв’язки може сполучатися з кожним
способами. При цьому кожна комбінація в середині зв’язки може сполучатися з кожним 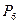 з способів утворення зв’язки, тобто
з способів утворення зв’язки, тобто 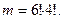
Отже,

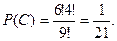
| <== попередня сторінка | | | наступна сторінка ==> |
| Опорний конспект лекцій | | | Дії над подіями та їх ймовірностями. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |