
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Свої набуті знання ви можете перевірити в наступному тесті
1.Якщо областю визначення функції є множина натуральних чисел, то функція називається...
а)натуральною функцією б)похідною послідовністю
в)первісною функцією г)числовою послідовністю
2.Якщо для будь-якого числа ε існує такий номер N, що при всіх n > N виконується нерівність |аn – а| < ε, то число а називається...
а)обмеженням послідовності б)розбіжністю послідовності
в)границею послідовності г)збіжністю послідовності
3.Якщо послідовність не має границю, то вона називається...
а)збіжною б)розбіжною
в)нескінченно малою г)нескінченно великою
4.Якщо границя послідовності дорівнює "+" або " – " нескінченності, то вона називається...
а)збіжною б)розбіжною
в)нескінченно малою г)нескінченно великою
5.Якщо для будь-якого члена послідовності виконується нерівність: наступний член менший за попередній, то послідовність називається...
а)зростаючою б)спадною
в)незростаючою г)неспадною
6.Якщо послідовність аn нескінченно мала, то послідовність 1/аn буде...
а)обмеженою б)необмеженою
в)нескінченно великою г)нескінченно малою
7.Добуток обмеженої послідовності на нескінченно малу буде послідовністю...
а)обмеженою б)необмеженою
в)нескінченно великою г)нескінченно малою
8.Якщо послідовність має границю, то вона...
а)обмежена б)необмежена
в)стала г)неперервна
9.Будь – яка збіжна послідовність ...
а)має тільки одну границю б)не має границі
в)має завжди дві границі г)є розбіжною
10.Границя суми двох нескінченно малих послідовностей є послідовністю...
а)обмеженою б)необмеженою
в)нескінченно великою г)нескінченно малою
Завдання для самоперевірки
1.Записати перші шість членів числової послідовності
а) хn = (2n + 1)/n б)уn = (n + (-1)nn)/n
2.Довести, що наступна послідовність не має границі
хn = (n + 1)/n, n = 1,3,5,….
1/n, n = 2,4,6,…
3.Куди прямують наступні послідовності?
а) хn = n!
б) yn = - n3
в) zn = n2cosπn.
Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001,
стор. 149 – 155.
Лекція „Послідовність. Границя послідовності і функції”
Означення. Якщо задана закономірність, згідно з якою кожному натуральному числу 1, 2, 3, …, відповідає деяке дійсне число, то говорять, що задано послідовність.
Послідовність можна розглядати як функцію, областю визначення якої є множина натуральних чисел.
Приклад. 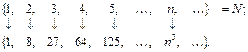
Послідовність визначається формулою, тобто законом, згідно з яким установлюється спосіб відповідності заданих чисел послідовним натуральним числам. Послідовність із загальним членом аn позначається 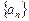 , або просто аn.
, або просто аn.
У прикладі: 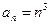 .
.
Інший спосіб визначення послідовності полягає в застосуванні рекурсії: n-й член послідовності визначається за допомогою заданих 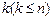 попередніх членів послідовності.
попередніх членів послідовності.
Приклад. Рекурсія 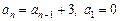 визначає послідовність 0, 3, 6, 9, ….
визначає послідовність 0, 3, 6, 9, ….
Приклад. Рекурсія 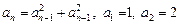 визначає послідовність 1, 2, 5, 27, 734, ….
визначає послідовність 1, 2, 5, 27, 734, ….
Приклади послідовностей.
1) 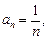
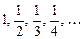 ; 2)
; 2) 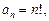
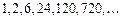 ;
;
3) 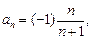
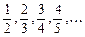 ; 4)
; 4) 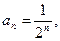
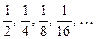 ;
;
Обмежені та монотонні послідовності
Означення. Послідовність 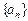 називається обмеженою, коли існує таке додатне число М, що нерівність
називається обмеженою, коли існує таке додатне число М, що нерівність
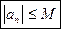
виконується для всіх n.
Означення. Послідовність 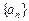 називається монотонно зростаючою (спадною), якщо
називається монотонно зростаючою (спадною), якщо
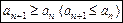
для всіх n.
Приклад. Визначити, які з наведених далі послідовностей обмежені, а які монотонні.
1) 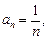 3)
3) 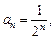
2) 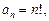 4)
4) 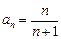 .
.
· За означенням відповідно обмеженої та монотонної послідовності маємо:
1) 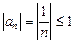 — обмежена послідовність;
— обмежена послідовність;
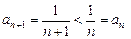 монотонна спадна послідовність;
монотонна спадна послідовність;
2) 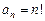 — необмежена послідовність;
— необмежена послідовність;
3) 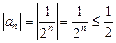 — обмежена послідовність;
— обмежена послідовність;
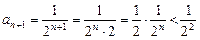 — монотонно спадна послідовність;
— монотонно спадна послідовність;
4) 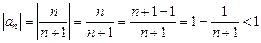 — послідовність обмежена;
— послідовність обмежена;
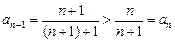 , оскільки
, оскільки
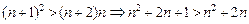 — послідовність монотонно зростаюча. ·
— послідовність монотонно зростаюча. ·
Означення. Послідовність хn називається обмеженою зверху, якщо існує число m, таке що при всіх n = 1, 2, 3, … виконується нерівність 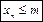 .
.
Означення. Послідовність хn називається обмеженою знизу, якщо існує число m, таке що при всіх n = 1, 2, 3, … виконується нерівність 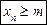 .
.
Означення. Послідовність хn, не обмежена зверху або знизу, називається необмеженою.
Приклад. Послідовність 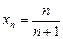 , для якої
, для якої
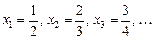
обмежена зверху та знизу: 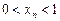 .
.
Приклад. Послідовність 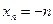 , тобто
, тобто
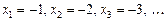
обмежена зверху, але не обмежена знизу.
Означення. Множина довільних точок Х на числовій осі називається обмеженою зверху, якщо існує число т, таке що для всіх 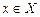 виконується нерівність
виконується нерівність 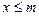 . Число т називається верхньою межею множини.
. Число т називається верхньою межею множини.
Означення. Множина довільних точок Х на числовій осі називається обмеженою знизу, якщо існує число m, таке що для всіх, 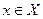 виконується нерівність
виконується нерівність 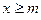 . Число m називається нижньою межею множини.
. Число m називається нижньою межею множини.
Множина, для якої існують верхня та нижня межі, називається обмеженою.
Найменша серед верхніх меж називається супремумом і позначається 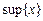 . Найбільша серед нижніх меж називається інфімумом і позначається
. Найбільша серед нижніх меж називається інфімумом і позначається 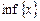 .
.
Означення. Точною верхньою межею множини Х називається значення 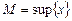 , таке що:
, таке що:
1) для будь-якого 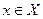 виконується нерівність
виконується нерівність 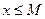 ;
;
2) для будь-якого 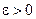 знайдеться значення
знайдеться значення 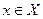 , таке що
, таке що
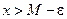 .
.
Аналогічно означується точна нижня межа множини Х.
Теорема.У будь-якої обмеженої множини існують точні верхня та нижня межі.
Збіжні та розбіжні послідовності
Означення. Число а називається границею послідовності 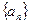 , якщо для кожного як завгодно малого додатного числа
, якщо для кожного як завгодно малого додатного числа 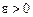 існує таке число
існує таке число 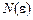 , що
, що
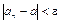 для всіх
для всіх 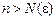 .
.
Позначення: 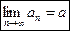 .
.
| <== попередня сторінка | | | наступна сторінка ==> |
| Тема 10 | | | Графічна ілюстрація |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |