
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Графічна ілюстрація
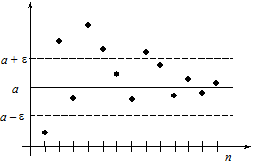 мал.. 1
мал.. 1
Означення. Послідовність, яка має границю, називається збіжною, а яка не має границі називається розбіжною.
Приклад. Послідовність 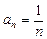 — збіжна, оскільки існує
— збіжна, оскільки існує 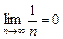 (за означенням
(за означенням 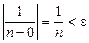 для будь-якого
для будь-якого 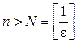 ).
).
Зауваження. Послідовність, границя якої дорівнює 0, називається нульовою послідовністю.
 Послідовність
Послідовність 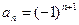 розбіжна, оскільки не має границі. Вона почергово набуває значення + 1 і – 1.
розбіжна, оскільки не має границі. Вона почергово набуває значення + 1 і – 1.
Властивості збіжних послідовностей
Теорема 1. Границя сталої дорівнює цій сталій:
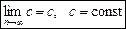 .
.
Теорема 2. Якщо послідовність хn має границю, то ця границя єдина.
Теорема 3. Послідовність хn, яка має границю, є обмеженою.
Теорема 4. Нехай 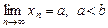 . Тоді знайдеться число N, таке що при будь-якому
. Тоді знайдеться число N, таке що при будь-якому 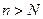 справджуватиметься нерівність
справджуватиметься нерівність 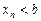 .
.
Теорема 5. Нехай 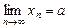 . Якщо послідовність xn при всіх n задовольняє нерівність
. Якщо послідовність xn при всіх n задовольняє нерівність 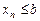 , то
, то 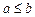 .
.
Теорема 6. Якщо 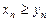 і
і 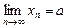 ,
, 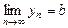 , то
, то 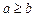 .
.
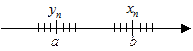
Означення. Перехід від нерівності 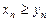 до нерівності
до нерівності 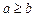 називається граничним переходом у нерівності.
називається граничним переходом у нерівності.
Теорема 7 (про «охоплену» послідовність або теорема про двох міліціонерів). Нехай виконується нерівність 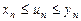 . Якщо послідовності хn і уn збіжні, причому
. Якщо послідовності хn і уn збіжні, причому 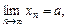
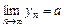 , то послідовність un також буде збіжною і
, то послідовність un також буде збіжною і 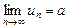 .
.
Приклад. Розглянемо послідовність 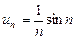 .
.
При всіх n виконується нерівність 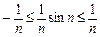 .
.
Оскільки 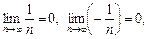 то
то 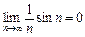 .·
.·
Теорема 8. (Больцано–Вейєрштрасса). Будь-яка монотонна обмежена послідовність має границю.
Число е
Розглянемо послідовність чисел 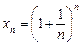 . Обчислимо кілька перших значень членів послідовності:
. Обчислимо кілька перших значень членів послідовності:
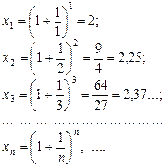
Доведемо, що послідовність хn монотонно зростає. За формулою бінома Ньютона маємо:
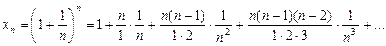
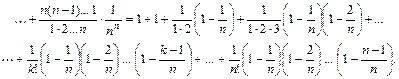 (3)
(3)
Замінимо в цьому розкладі n на n + 1. Тоді число доданків збільшиться на одиницю.
Далі маємо:
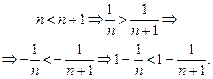
Кожний вираз, що містить n, зростає, тобто 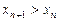 .
.
Доведемо обмеженість послідовності хn.
У формулі (3) значення кожного виразу в дужках менше від одиниці. Отже,
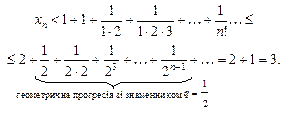
За формулою суми геометричної прогресії маємо:
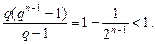
Звідси
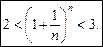
За теоремою Больцано–Вейєрштрасса послідовність 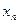 має границю.
має границю.
Означення. Границя послідовності 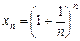 називається числом е.
називається числом е.
Позначення:
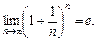
Число е* — (так зване Неперове число).
Для кращого розуміння означення границі послідовності розглянемо приклади:
Приклад.Використовуючи означення границі послідовності довести, що 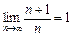 .
.
Згідно з означенням границі послідовності для довільного 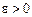 треба знайти такий номер елемента послідовності N, що для всіх
треба знайти такий номер елемента послідовності N, що для всіх 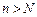 виконувалася б нерівність
виконувалася б нерівність 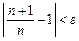 . Нехай вибрано
. Нехай вибрано 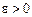 , за цим e розглянемо
, за цим e розглянемо 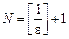 , тоді
, тоді 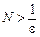 і для будь-якого
і для будь-якого 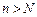 маємо:
маємо: 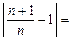
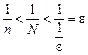 .
.
Проілюструємо одержаний результат табличкою:
| e | 0,5 | 0,1 | 0,01 | 0,001 | 0,0001 | … |
| N | … |
Тоді при 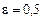 , починаючи з
, починаючи з 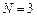 , відповідні п можна брати з послідовності
, відповідні п можна брати з послідовності 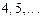 Для них
Для них 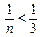 . Якщо
. Якщо 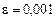 , а
, а 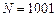 , то тепер п можна брати з послідовності
, то тепер п можна брати з послідовності 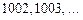 і знову нерівність
і знову нерівність 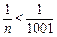 виконується. Отже, для будь-якого навіть нескінченно малого значення e можна знайти N, що для всіх
виконується. Отже, для будь-якого навіть нескінченно малого значення e можна знайти N, що для всіх 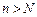 нерівність
нерівність 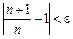 виконується. Це й означає, що
виконується. Це й означає, що 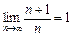 .
.
Приклад.Використовуючи означення границі функції, довести, що 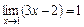 .
.
Згідно з означенням границі функції для будь-якого 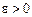 треба знайти таке
треба знайти таке 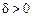 , що для тих х, для яких виконується не-
, що для тих х, для яких виконується не-
рівність 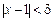 , виконується й нерівність
, виконується й нерівність 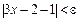 . Нехай вибрано деяке
. Нехай вибрано деяке 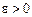 , за ним знайдемо
, за ним знайдемо 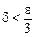 . Тоді
. Тоді 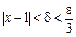 .
.
Повернемося до нерівності: 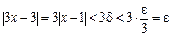 . Тобто
. Тобто
доведено, що 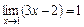 .
.
З наведених прикладів зрозуміло, що завдання знаходження границі послідовності і функції з використанням означення досить складне. Формально для знаходження границі треба у вираз функції підставити число, до якого прямує х. Якщо в результаті підстановки одержується число, то воно дорівнює границі функції, але, як правило, за такої підстановки одержують так звану невизначеність вигляду: 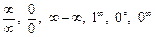 і т. п. Для розкриття невизначеності дещо перетворюють вираз функції, що стоїть під знаком границі, і використовують відповідні теореми теорії границь або одну з особливих границь.
і т. п. Для розкриття невизначеності дещо перетворюють вираз функції, що стоїть під знаком границі, і використовують відповідні теореми теорії границь або одну з особливих границь.
Приклади. Знаходження границь:
1) 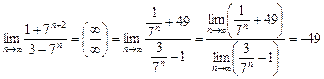 .
.
2) 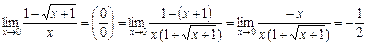 .
.
3) 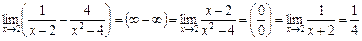 .
.
4) 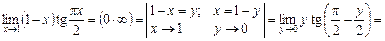
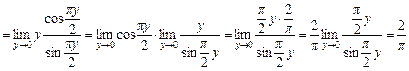 .
.
5) 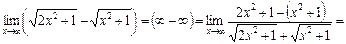
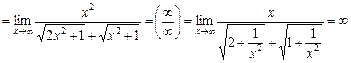 .
.
6) 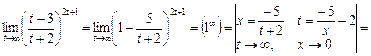
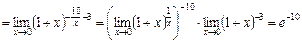 .
.
7) 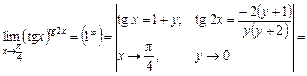
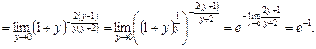
Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001,
стор. 149 – 155.
Тема 11
| <== попередня сторінка | | | наступна сторінка ==> |
| Свої набуті знання ви можете перевірити в наступному тесті | | | Неперервність функції в точці і на проміжку. Точки розриву |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |