
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Тема 13
Диференціал функції, його геометричний зміст. Властивості. Застосування диференціала в наближених обчисленнях
Мета заняття Засвоєння поняття диференціалу функції в точці; формування уміння знаходити диференціали та застосовувати їх при наближених обчисленнях.
Виховувати розумову культуру, культуру усного і писемного мовлення; розвивати логічне мислення.
Студенти повинні знати: поняття диференціалу функції, його геометричний зміст, властивості.
Студенти повинні вміти: знаходити диференціал функції, застосовувати його в наближених обчисленнях.
Основні питання теми
Ми знаємо, що процес знаходження похідних називається диференціюванням. Але в математичному аналізі є поняття диференціала функції в точці як самостійне. Що це таке і для чого, ви повинні вивчити в цій темі
1.Поняття диференціала функції в точці; позначення;
2.Властивості диференціала;
3.Геометричний зміст диференціала;
4.Застосування диференціала в наближених обчисленнях;
5.Приклади
Завдання для самоперевірки
Закінчте вирази:
1. Похідною функції 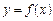 у точці х називається
у точці х називається
2. Дотичною до графіка функції 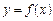 у точці М називається …
у точці М називається …
3. Геометричний зміст похідної функції полягає в тому, що …
4. Фізичний зміст похідної функції полягає в тому, що …
5. Економічний зміст похідної функції полягає в тому, що …
6. Функція 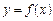 називається диференційовною в точці х, якщо …
називається диференційовною в точці х, якщо …
7. Вказати правильне твердження:
а) якщо функція 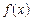 неперервна в точці х, то вона диференційовна в ній;
неперервна в точці х, то вона диференційовна в ній;
б) якщо функція 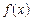 диференційовна в точці х, то вона неперервна в цій точці.
диференційовна в точці х, то вона неперервна в цій точці.
8. Диференціалом функції 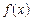 називається …
називається …
9. Геометричний зміст диференціала полягає в тому, що …
10. Якщо існують похідні функцій 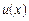 і
і 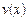 , то:
, то:
а) 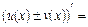 … (довести);
… (довести);
б) 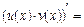 … (довести);
… (довести);
в) 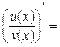 … (довести).
… (довести).
11. Сформулювати і довести теорему про похідну складної функції.
12. Сформулювати і довести теорему про похідну оберненої функції.
13. Еластичністю функції називається …
14. Якщо існують еластичності 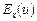 та
та 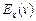 функцій
функцій 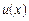 і
і 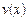 , то:
, то:
а) 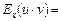 … (довести);
… (довести);
б) 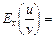 … (довести).
… (довести).
15. Попит називається еластичним, якщо …
16. Попит називається нееластичним, якщо …
17. Знайти відношення 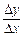 для функцій:
для функцій:
1) 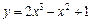 при
при 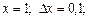
2) 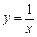 при
при 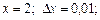
3) 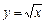 при
при 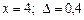 .
.
18. Використовуючи означення похідної як 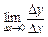 , знайти похідні функцій:
, знайти похідні функцій:
1) 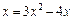 ; 2)
; 2) 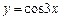 ;
;
3) 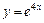 ; 4)
; 4) 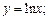
5) 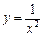 ; 6)
; 6) 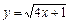 ;
;
7) 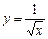 ; 8)
; 8) 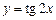 .
.
19. Нехай витрати виробництва є функцією кількості випущеної продукції: 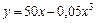 . Знайти середні і граничні витрати виробництва за обсягу випущеної продукції, що дорівнює 10 грошовим одиницям.
. Знайти середні і граничні витрати виробництва за обсягу випущеної продукції, що дорівнює 10 грошовим одиницям.
20. Обсяг виготовленої продукції у (ум. од.) цеху протягом робочого дня виражається такою функцією 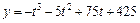 , де t — кількість годин роботи. Знайти обсяг випуску продукції через 2 години після початку робочого дня.
, де t — кількість годин роботи. Знайти обсяг випуску продукції через 2 години після початку робочого дня.
21. У якій точці дотична до параболи 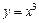 : 1) паралельна осі ОХ; 2) утворює кут 45° з віссю ОХ?
: 1) паралельна осі ОХ; 2) утворює кут 45° з віссю ОХ?
22.Знайти диференціал функції у = lnsin 2х: а)при довільних значеннях х і Δх; б)при х = π/8; в) при х = π/8 і Δх = 0,1.
23.Обчислити наближено arсtg 1,05.
24.Знайти диференціал функції у = lnsin 2х: а)при довільних значеннях х і Δх; б)при х = π/8; в) при х = π/8 і Δх = 0,1.
25.Обчислити наближено arсtg 1,05.
Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001,
гл.5, стор. 218 – 222.
Лекція „диференціал”
Нехай функція у = f(x) диференційовна в інтервалі 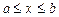 .
.
З означення диференційовності маємо:
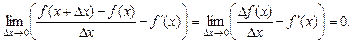
Звідси можна записати:
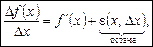 (1)
(1)
де функція  при
при 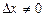 задовольняє умову
задовольняє умову
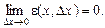
Із (1) для приросту функції дістаємо:
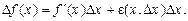
Покладемо, що 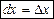 .
.
Означення. Величина f¢(x)Dх називається диференціалом функції f(x) за приростом Dх.
Позначення: 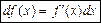
Геометрична інтерпретація:
Диференціал 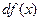 є лінійним наближенням (апроксимацією) до приросту функції:
є лінійним наближенням (апроксимацією) до приросту функції: 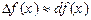 . Наскільки менше
. Наскільки менше 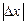 , настільки краще наближення (апроксимація) (мал. 1).
, настільки краще наближення (апроксимація) (мал. 1).
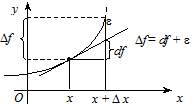 мал. 1
мал. 1
Приклад. Нехай 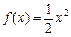 . Знайдемо диференціал df(x) і приріст Df(x) для
. Знайдемо диференціал df(x) і приріст Df(x) для 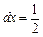 і
і 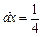 і порівняємо їх.
і порівняємо їх.

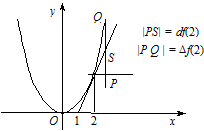 мал. 2
мал. 2
1)  ;
;
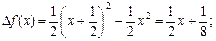
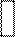
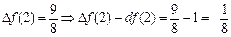 (мал. 2).
(мал. 2).
2) 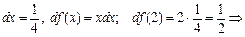
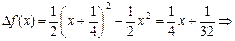
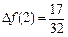 .
.

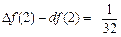 . ·
. ·
Правила обчислення диференціала
Правило 1. Нехай 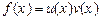 .
.
Тоді 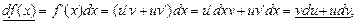
або
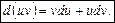
Правило 2. Дано 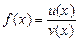 .
.
Тоді 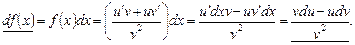
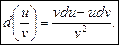
Правило 3. Маємо 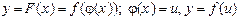 ,
,  .
.
Тоді
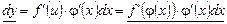
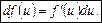
Правило 4. Якщо 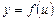 ,
, 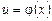 , то
, то
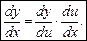
Правило 5. Якщо функція 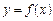 має обернену
має обернену 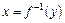 , то
, то
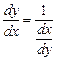 .
.
Правило 6. Якщо функції задані у параметричному вигляді
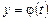 ,
,  ,
,
то
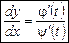 .
.
Зауваження. Такі перетворення застосовують, виконуючи інтегрування функцій.
Інваріантність форми
першого диференціала функції
Важлива властивість диференціала функції полягає в тому, що його вигляд лишається незмінним навіть у тому разі, коли переходять до іншої незалежної змінної.
¨ Справді, нехай у = f(x). Тоді диференціал цієї функції записується у вигляді
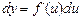 . (1)
. (1)
Виконаємо заміну змінних u = j(x). Тоді функція у = f(u) буде функцією від змінної х:
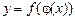 .
.
Обчислюючи диференціал цієї функції, дістаємо:
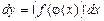 , (2)
, (2)
або
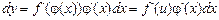 . (3)
. (3)
Вираз 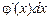 є диференціалом функції u, оскільки
є диференціалом функції u, оскільки 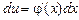 . Тому (3) можна подати у вигляді
. Тому (3) можна подати у вигляді
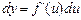 .
.
Отже, ми повернулися до вигляду диференціала (1), який був записаний за припущення, що змінна u є незалежною. Маємо властивість диференціала, яка називається його інваріантністю:
| <== попередня сторінка | | | наступна сторінка ==> |
| Похідні тригонометричних функцій | | | Формула для знаходження диференціала |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |