
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Тема 14
Формула Тейлора
Мета заняття :вивести формулу Тейлора представлення функції у вигляді многочлена . Розвивати логічне мислення.
Студенти повинні знати: формулу Тейлора представлення функцій у вигляді многочлена.
Студенти повинні вміти: знаходити похідні вищих порядків функцій; користуватися формулою Тейлора представлення функцій у вигляді многочлена; записувати розкладання елементарних функцій за формулою Тейлора.
Основні питання теми
1.Формула Тейлора;
2.Формула Маклорена;
3.Приклади
Завдання для самоперевірки
1.За правилом Лопіталя обчислити границі
1. 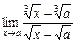 . 2.
. 2. 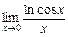 .
.
3. 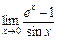 . 4.
. 4. 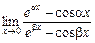 .
.
5. 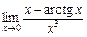 . 6.
. 6. 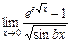 .
.
7. 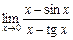 . 8.
. 8.  .
.
9. 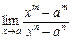 . 10.
. 10. 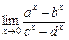 .
.
11. 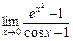 . 12.
. 12. 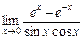 .
.
13. 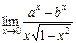 . 14.
. 14. 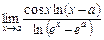 .
.
15.  . 16.
. 16. 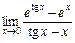 .
.
2.Записати формулу Тейлора для наступних функцій
1. Розкласти многочлен 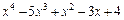 за степенями двочлена
за степенями двочлена 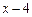 .
.
2. Розкласти многочлен 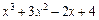 за степенями двочлена
за степенями двочлена 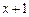 .
.
3. Розкласти многочлен 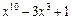 за степенями двочлена
за степенями двочлена 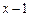 .
.
4. Функцію 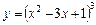 розкласти за степенями х, використовуючи формулу Тейлора.
розкласти за степенями х, використовуючи формулу Тейлора.
5. Записати формулу Тейлора п-го порядку для функції 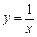 при
при 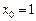 .
.
6. Записати формулу Маклорена п-го порядку для функції 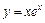 .
.
7. Записати формулу Тейлора п-го порядку для функції 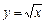 при
при 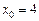 .
.
8. Записати формулу Маклорена 2п-го порядку для функції  .
.
9. Записати формулу Тейлора п-го порядку для функції  при
при 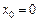 .
.
10. Записати формулу Маклорена 2п-го порядку для функції  .
.
11. Записати формулу Тейлора 3-го порядку для функції 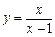 при
при  . Побудувати графіки цієї функції і її много-
. Побудувати графіки цієї функції і її много-
члена 3-го порядку.
12. Записати формулу Тейлора 2-го порядку для функції 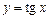 при
при 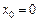 і побудувати графіки цієї функції і її многочлена 2-го порядку.
і побудувати графіки цієї функції і її многочлена 2-го порядку.
Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001
Гл.5, стор. 238 – 245.
Лекція „Формула Тейлора”
Нехай функція f(x) має п похідних у точці х0.
Означення. Многочлен
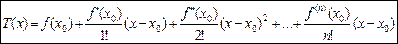
називається многочленом Тейлора функції f(x) у точці х0.
Теорема. Нехай функція f(x) має в e-околі точки х0 (n + 1) похідну. Тоді для будь-якої точки х із цього околу знайдеться точка с, розміщена між точками х і х0, для якої справджується рівність:
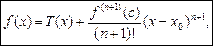 (1)
(1)
де Т(х) — п-й многочлен Тейлора функції f(x) у точці х0.
Формула (1) називається формулою Тейлора.
Беручи у формулі (1) х0 = 0, дістанемо формулу, яку називають формулою Маклорена:
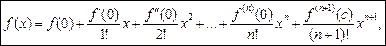
де с — точка, розміщена між 0 і х.
Застосування формули Тейлора
в економічних задачах
1. Рівність 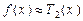 застосовується в задачах економічної статистики. Наприклад, розглянемо таку задачу.
застосовується в задачах економічної статистики. Наприклад, розглянемо таку задачу.
Задача. Припустимо, що для чисел відомо середнє арифметичне
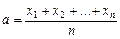
і середнє квадратичне відхилення:
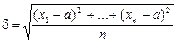 .
.
Як визначити середнє арифметичне виду
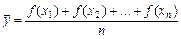 ,
,
якщо числа х1, х2, …, хn невідомі, але відомий відрізок, якому вони належать?
· Значення 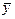 можна, очевидно, знайти лише наближено. При цьому похідна буде настільки малою, наскільки малим буде максимальне значення
можна, очевидно, знайти лише наближено. При цьому похідна буде настільки малою, наскільки малим буде максимальне значення 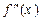 на відрізку, який містить х1, х2, …, хn.
на відрізку, який містить х1, х2, …, хn.
Замінимо функцію f(x) на многочлен Тейлора другого порядку в точці а:
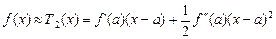 .
.
Тоді
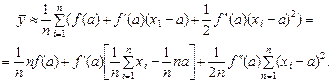
Оскільки
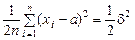 ,
,
маємо:
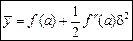 . ·
. ·
Приклад. Для додатних чисел х1, х2, …, хn відоме середнє арифметичне а і середнє квадратичне відхилення δ. Знайти наближено середнє геометричне 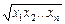 .
.
· Середнє геометричне можна подати у вигляді:
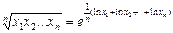 .
.
Використовуючи формулу (7) для функції 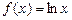 , одержимо
, одержимо
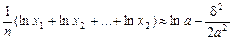 .
.
Отже, середнє геометричне дорівнює
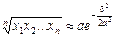 .
.
Приклад. Нехай рі — вартість споживчого кошика на 1 січня і-го року, 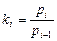 — індекс споживчих цін за цей рік. Відомо, що середнє арифметичне чисел k1, k2, …, kn дорівнює 1, а середнє квадратичне відхилення δ = 1. Визначити відносну зміну споживчих цін з 1 січня і-го року по 1 січня (і+10)го року.
— індекс споживчих цін за цей рік. Відомо, що середнє арифметичне чисел k1, k2, …, kn дорівнює 1, а середнє квадратичне відхилення δ = 1. Визначити відносну зміну споживчих цін з 1 січня і-го року по 1 січня (і+10)го року.
· Згідно з формулою (8) знаходимо
 .
.
Далі маємо:
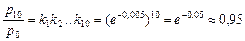 .
.
Отже, ціни за 10 років зросли приблизно на 5%. ·
Розклад основних елементарних функцій
за формулою Тейлора
1. Розкладемо за формулою Тейлора функцію 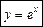 у
у
т. х0 = 0. Для цього обчислюємо:
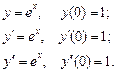
Далі за формулою Тейлора (1) маємо:
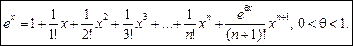
Зокрема, при х = 1
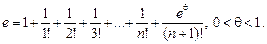
У цьому розкладі залишковий член прямує до нуля при 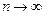 :
:
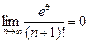 .
.
Можна записати: 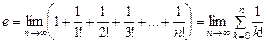 .
.
Цей вираз називають рядами і позначають так:
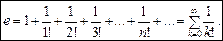
2. Розкладемо за формулою Тейлора функцію 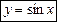 у
у
т. х0 = 0. Насамперед знайдемо:
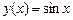 ,
, 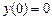 ;
;
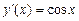 ,
, 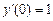 ;
;
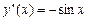 ,
, 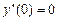 ;
;
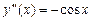 ,
, 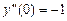 ;
;
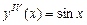
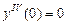 ;
;
..................................................................................
За формулою Тейлора (1) дістанемо (мал. 1)
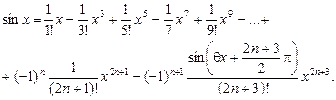
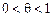 .
.
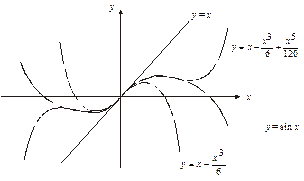
мал. 1
3. Розклад за формулою Тейлора функції 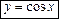 в т. х0 = 0.
в т. х0 = 0.
Насамперед обчислимо:
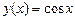 ,
, 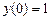 ;
;
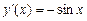 ,
, 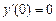 ;
;
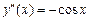 ,
, 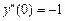 ;
;
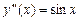 ,
, 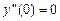 ;
;
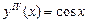 ,
, 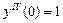 .
.
Далі за формулою Тейлора (1) дістанемо:
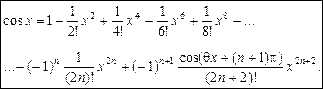
Приклад. Знайдемо значення 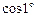 з точністю до 10–10.
з точністю до 10–10.
● Оскільки 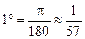 , то
, то
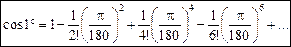
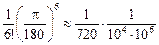 .
.
Щоб досягти заданої точності, візьмемо
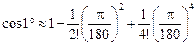 ●
●
Розклад за формулою Тейлора
деяких часто застосовуваних функцій
1. Розклад функції 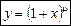 ,
, 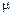 — довільне число.
— довільне число.
Насамперед
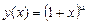 , ,
| 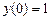 ; ;
|
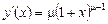 , ,
| 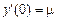 ; ;
|
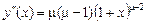 , ,
| 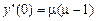 ; ;
|
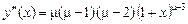 , ,
| 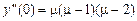 . .
|
....................................................................................
За формулою Тейлора отримаємо розклад
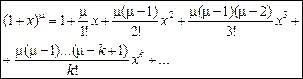
Цей розклад названо формулою бінома Ньютона на честь її відкривача. Якщо 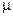 — натуральне число, то розклад містить скінченне число доданків.
— натуральне число, то розклад містить скінченне число доданків.
.
2. Розклад функції 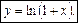
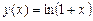 , ,
| 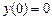 ; ;
|
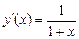 , ,
| 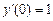 ; ;
|
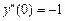 ; ;
| |
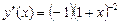 , ,
| 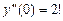 ; ;
|
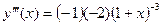 , ,
| 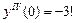 ; ;
|
| … … … … … … | … … … … … … |
За формулою Тейлора (1) дістанемо розклад
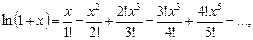
або 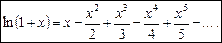
Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001
Гл.5, стор. 238 – 245.
| <== попередня сторінка | | | наступна сторінка ==> |
| Формула для знаходження диференціала | | | Тема 15 |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |