
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Тема 16
Функція багатьох змінних. Означення та символіка. Границя функції. Графік функції
Мета заняття Формування первинних уявлень про функцію двох (трьох) змінних та її графік, умінь знаходити області визначення та множину значень функції двох змінних.
Розвивати логічне мислення, допитливість.
Студенти повинні знати: означення функції багатьох змінних; поняття області визначення та множини значень функції; поняття графіка функції двох та трьох змінних; та символіку теми.Студенти повинні вміти: відрізняти функції багатьох змінних, знаходити та зображувати області визначення та множини значень функцій двох та трьох змінних;
Основні питання теми
До теперішнього часу ми розглядали та вивчали функцію однієї змінної х. Але в природі існує багато процесів і залежностей, коли, щоб отримати результати того чи іншого процесу, необхідно мати дані двох, трьох або більше параметрів. Отже, існують функції, які залежать від двох або більше змінних.
1.Означення функції двох змінних; приклади;
2.Область визначення та множина значень;
3.Межа області визначення; відкриті та замкнені області; приклади;
4.Графік функції двох змінних; лінії рівня;
5.Границя функції багатьох змінних;
6.Неперервність функції багатьох змінних;
7.Приклади
Завдання для самоперевірки
1.Знайти область визначення D функції
z = 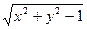 + ln(4 – х2 – у2)
+ ln(4 – х2 – у2)
2.Дослідити на неперервність функції
а) z = 2х2 + 3у; б) z = (х + у – 1)/(у2 – 2х).
3.Знайти та зобразити області визначення функцій двох змінних:
1. 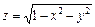 . 2.
. 2. 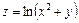 .
.
3. 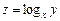 . 4.
. 4. 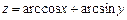 .
.
5. 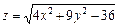 . 6.
. 6. 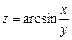 .
.
7. 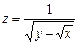 . 8.
. 8. 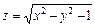 .
.
9. 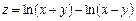 . 10.
. 10. 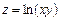 .
.
11. 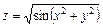 . 12.
. 12. 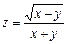 .
.
13. 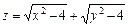 . 14.
. 14. 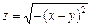 .
.
Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001
гл.6, стор. 284 – 294.
Лекція „Означення функції багатьох змінних”
Означення. Якщо кожній точці множини D n-вимірного простору Rn за деяким законом Р(х1, х2, …, хn) поставлено у відповідність одне і тільки одне дійсне число 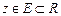 , то говорять, що в області
, то говорять, що в області 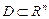 задано функцію n незалежних змінних.
задано функцію n незалежних змінних.
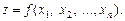
При цьому D називають областю визначення функції, а Е — областю значень функції.
Згідно з означенням функцію 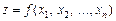 можна розглядати як функцію точки і записувати як
можна розглядати як функцію точки і записувати як 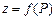 .
.
Зокрема, коли n = 2, маємо функцію двох змінних 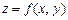 , якщо кожній парі
, якщо кожній парі 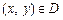 на площині поставлено у відповідність одне і тільки одне число z.
на площині поставлено у відповідність одне і тільки одне число z.
Зауважимо, що в задачах економічного змісту найчастіше доводиться стикатися з функціями двох або трьох незалежних змінних. Тому надалі головну увагу приділятимемо саме їм.
Наведемо приклади таких функцій.
Приклад. Витрати виробництва даного виробу за даної технології є функцією матеріальних витрат х і витрат у на оплату робочої сили: 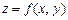 . Це є функція витрат виробництва.
. Це є функція витрат виробництва.
Приклад. Розглянемо функцію двох незалежних змінних K, L, яка називається виробничою функцією, або функцією Кобба—Дугласа: 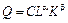 ,
, 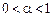 ;
; 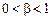 , де Q — обсяг виробництва; С — деяка стала; L — кількість праці, яку вкладено у виробництво; K — кількість капіталу. Із наведеної рівності випливає, що частка, %, заробітної плати в загальному прибутку становить a × 100, а частка капіталу, %, b × 100. Задану функцію можна подати у вигляді таблиці або графіка. Для двох факторів таким графіком може бути рівнопродуктова крива, для більшої їх кількості — деякий тривимірний образ.
, де Q — обсяг виробництва; С — деяка стала; L — кількість праці, яку вкладено у виробництво; K — кількість капіталу. Із наведеної рівності випливає, що частка, %, заробітної плати в загальному прибутку становить a × 100, а частка капіталу, %, b × 100. Задану функцію можна подати у вигляді таблиці або графіка. Для двох факторів таким графіком може бути рівнопродуктова крива, для більшої їх кількості — деякий тривимірний образ.
Криву, що являє собою множину точок, кожною з яких подається одна з можливих комбінацій двох факторів виробництва, котрі забезпечують однакову кількість виготовлюваної продукції, зображено на мал. 1.
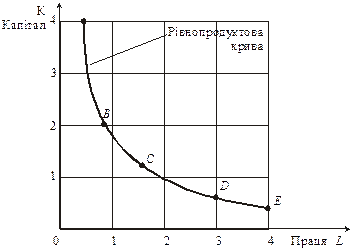
мал. 1.
Приклад.
Нехай предметами споживання є два товари А — масло та В — маргарин, ціни на які становлять відповідно р1 та р2. Якщо ціни на інші товари сталі, а прибуток споживачів і структура споживання не змінюються, то попит і пропозиція за кожним із товарів залежать від його ціни. Маємо:
функцію попиту на товар А: q1 = f1(p1, p2);
функцію попиту на товар В: q2 = f2(p1, p2);
функцію пропозиції товару А: s1 = f3(p1, p2);
функцію пропозиції товару В: s2 = f4(p1, p2).
Задану умовою задачі залежність можна подати такою таблицею:
| Характеристика товару | Товар А — масло | Товар В — маргарин |
| Кількість | q1 | q2 |
| Ціна | p1 | p2 |
Попит на масло визначатиметься функцією 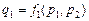 і залежатиме від його ціни р1 та ціни р2 конкурентного товару — маргарину.
і залежатиме від його ціни р1 та ціни р2 конкурентного товару — маргарину.
Зокрема, ця функція може набирати такого вигляду:
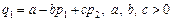 ,
,
або 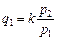 .
.
| <== попередня сторінка | | | наступна сторінка ==> |
| Свої набуті знання ви можете перевірити в наступному тесті | | | Способи задання функції |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |