• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Частинні похідні і повні диференціали вищих порядків

Нехай функція 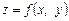має частинні похідні в усіх точках множини D. Візьмемо будь-яку точку 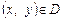. Якщо в цій точці існують частинні похідн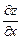і і 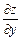, то вони залежать від х і у, тобто вони є функціями двох змінних. Отже, можна ставити питання про відшукання їх частинних похідних. 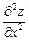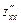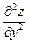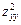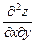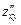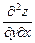Якщо вони існують, їх називають частинними похідними другого порядкуі позначають відповідно (читаємо: «де два зет по де ікс квадрат») або , або , або , або 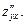Аналогічно визначаються і позначаються частинні похідні третього і вищих порядків.

Нехай функція 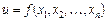в околі точки 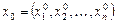має частинну похідну першого порядку .

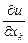Означення. Частинну похідну функції 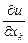за змінною 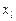називають частинною похідною другого порядку за змінними 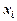і 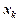і позначають 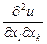або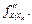

Отже, за означенням:

.

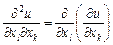Якщо 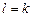, похідну 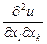позначають .

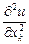Означення. Частинною похідною порядку 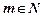називають частинну похідну першого порядку за будь-якою змінною від будь-якої похідної 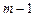порядку.

Частинні похідні за різними змінними називають мішаними частинними похідними.

Теорема . Якщо дві мішані похідні порядку m, що відріз­няються лише порядком диференціювання, неперервні в деякій точці, то їх значення в цій точці збігаються.

Приклад. Знайти 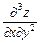, якщо .

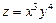●Маємо: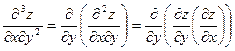

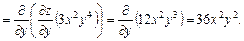
Знайти 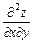і 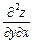для функції .

● .

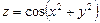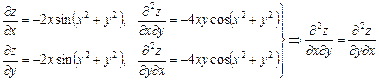Означення. Диференціалом другого порядку функції 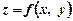називається диференціал її повного диференціала:

.

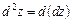Аналогічно визначаються диференціали третього і вищих порядків:

.

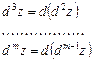Для диференціала порядку m справджується залежність:

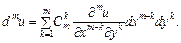(6)

У частинному випадку при 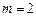формула (8) набирає вигляду:

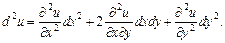(7)

Зауваження. Для складеної функції 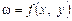, де 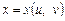, , 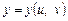другий її диференціал, загалом, не подається через dx і dy згідно з формулою (9). Отже, для порядку 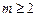не виконується властивість інваріантності форми диференціала щодо вибору змінних.

У разі функції n змінних 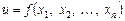формула (8) набирає вигляду:

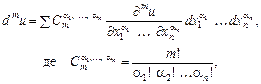(8)

де підсумовування виконується за всіма цілими невід’ємними 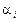, такими що .

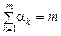При 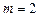формула (8) подається так:

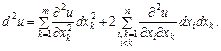
Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001

Гл.6, стор. 294- 318.

Переглядів: 1342