
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Тема 19
Поняття первісної функції та невизначеного інтегралу. Таблиця основних інтегралів
Мета заняття Узагальнити та систематизувати знання з теми.
Розвивати уважність, вміння самостійно визначати головну думку, логічне мислення.
Студенти повинні знати: поняття первісної функції та невизначеного інтегралу, властивості невизначеного інтегралу;основні табличні інтеграли.
Студенти повинні вміти: знаходити первісні функції та невизначені інтеграли; використовувати властивості для знаходження первісних та інтегралів.
Основні питання теми
1.Поняття первісної; властивості первісної;
2.Невизначений інтеграл; позначення, властивості;
3.Застосування інваріантності форми першого диференціалу при інтегруванні;
4.Таблиця основних інтегралів;
5.Приклади.
Свої набуті знання ви можете перевірити в наступному тесті
1.Якщо функція F(х) диференційовна на (а;b) і її похідна дорівнює f(х),то вона називається..........
а)оберненою до f(х) б)складеною на (а;b)
в)первісною для f(х) г)розривною на (а;b)
2.Якщо функція f(х) має первісну F(х), то вона має........
а)множину первісних F(х) + С б)обернену функцію F(х) + С
в)складену функцію F(х) + С г)розривну функцію f(х) + С
3.Множина усіх первісних функції f(х) називається.........
а)визначеним інтегралом функції f(х)
б)невизначеним інтегралом функції f(х)
в)криволінійним інтегралом функції f(х)
г)невласним інтегралом функції f(х)
4.Сталий множник можна виностит за знак.......
а)похідної
б)первісної
в)інтеграла
г)функції
Завдання для самоперевірки
1.Сформулювати теорему про існування первісної.
2.У чому суть інваріантності формули інтегрування? Навести приклади.
3.Закінчте вирази:
- Первісною називається …
- Операції знаходження для функції похідної і первісної співвідносяться між собою як …
- Теорема про множину первісних функції формулюється так: …
- Задача інтегрування функції на деякому проміжку полягає в тому, щоб -Теоретичною основою розв’язання задачі інтегрування функції є теорема про …
- Невизначеним інтегралом називається …
4. Які з наведених нижче функцій будуть первісними для функції 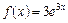 ?
?
а) 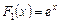 ; б)
; б) 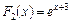 ;
;
в) 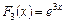 ; г)
; г) 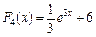 ;
;
д) 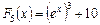 .
.
(Зазначте правильну відповідь.)
5. Які з наведених функцій будуть первісними для функції 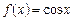 ?
?
а) 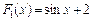 ; б)
; б) 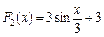 ;
;
в) 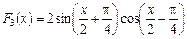 .
.
Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001
Гл.7, стор. 330 – 336.
Лекція „Поняття невизначеного інтеграла”
Означення. Нехай функція f (x) є похідною від функції F (x), тобто f (x)dx — диференціал функції F (x):
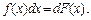
Тоді функція F (x) називається первісною для функції f (x).
Якщо F (x) — одна з первісних функції f (x), то будь-яка інша її первісна подається виразом F (x) + С, де С — довільна стала.
Отже, якщо функція f (x) має принаймні одну первісну, то їх існує безліч.
Означення. Найзагальніший вигляд первісної для даної функції f (x) (або даного виразу f (x)dx) називається її невизначеним інтегралом.
Невизначений інтеграл виразу f (x)dx позначають
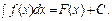 (1)
(1)
Термін «інтеграл» походить від латинського слова integralis — цілісний.
Символ 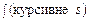 — початкова літера слова summa (сума).
— початкова літера слова summa (сума).
Слово «невизначений» підкреслює, що до загального виразу первісної входить сталий доданок, який можна взяти довільно.
Вираз 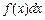 називають підінтегральним виразом, функцію f (x) — підінтегральною функцією, змінну x — змінною інтегрування.
називають підінтегральним виразом, функцію f (x) — підінтегральною функцією, змінну x — змінною інтегрування.
Постають такі запитання: 1) чи завжди можна знайти невизначений інтеграл; 2) як можна знайти цей інтеграл, якщо він існує?
Відповідь на перше запитання частково дає наведена далі теорема, яка є основною теоремою інтегрального числення.
Теорема 1. Усяка неперервна функція має первісну.
Проте ця теорема не стверджує, що первісну даної неперервної функції можна знайти за допомогою скінченної кількості відомих дій і подати результат в елементарних функціях. Більш того, існують неперервні елементарні функції,інтеграли від яких не є елементарними функціями. Такі функції називають неінтегровними. Їх інтеграли не можуть бу-
ти знайдені за допомогою скінченної кількості елементарних функцій.
Наприклад, можна довести, що інтеграли 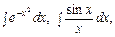
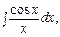
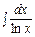 не подаються елементарними функціями, тобто відповідні підінтегральні функції є неінтегровними.
не подаються елементарними функціями, тобто відповідні підінтегральні функції є неінтегровними.
Зауважимо, що за правилами диференціального числення для будь-якої елементарної функції можна знайти її похідну (також елементарну). В інтегральному численні такі правила для відшукання первісної принципово неможливі.
Первісні для неінтегровних функцій, таких як 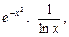
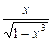 і т. ін., знаходять наближеними (чисельними) методами.
і т. ін., знаходять наближеними (чисельними) методами.
Загалом знаходження невизначених інтегралів — задача, істотно складніша порівняно з диференціюванням. Її розв’язування спрощується завдяки застосуванню математичних довідників і комп’ютерних пакетів програм, наприклад Mathсad, Mathematica 3.0 тощо.
| <== попередня сторінка | | | наступна сторінка ==> |
| Тема 18 | | | Основні властивості невизначеного інтеграла |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |