
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Тема 20
Означення та умови існування визначеного інтегралу. Властивості. Формула ньютона – Лейбніца
Мета заняття Узагальнити та систематизувати знання з теми.
Розвивати уважність, вміння самостійно визначати головну думку, логічне мислення.
Студенти повинні знати: означення та умови існування визначеного інтеграла; властивості визначеного інтеграла, формулу Ньютона-Лейбница.
Студенти повинні вміти: обчисляти визначені інтеграли; застосовувати властивості визначеного інтеграла для його обчислення.
Основні питання теми
1.Задачі, що приводять до визначеного інтеграла (про площу криволінійної трапеції, про роботу змінної сили, про пройдений шлях, про масу неоднорідного стержня);
2.Означення та умови існування визначеного інтеграла;
3.Властивості визначеного інтеграла;
4.Формула Ньютона – Лейбніца;
5.Геометричний зміст визначеного інтеграла;
6.Фізичний зміст визначеного інтеграла;
7.Необхідна та достатня умови інтегрованості;
8.Теорема про середнє значення функції;
9.Приклади.
Завдання для самоперевірки
1.Сформулювати теорему про існування визначеного інтеграла.
2.Сформулювати і довести властивості аддитивності і збереження знака визначеного інтеграла.
3.Із фігур, що обмежені лініями:
а) 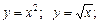 б)
б) 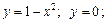
в) 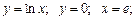 г)
г) 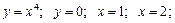
д) 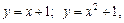
виберіть ті, які не відповідають поняттю «криволінійна трапеція».
4. Визначеним інтегралом називається …
5.Геометричний зміст визначеного інтеграла полягає в тому, що …
6. Виберіть правильні твердження. Величина визначеного інтеграла залежить від: а) виду підінтегральної функції; б) позначення аргументу; в) проміжку інтегрування; г) області визначення первісної функції.
7.Теорема про середнє для визначеного інтеграла формулюється так …
8.Сформулюйте п’ять будь-яких властивостей визначеного інтеграла.
9. Які з формул:
а) 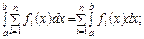 б)
б) 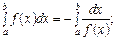
в) 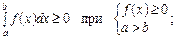 г)
г) 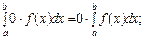
д) 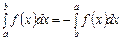
відбивають властивості визначеного інтеграла?
10.Обчислити інтеграли
б) 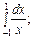 в)
в) 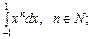
е) 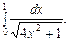
Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001, стор.365 – 380.
Лекція „Визначений інтеграл”
І. Поняття визначеного інтеграла.
Означення. Сума 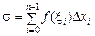 називається інтегральною сумою, або сумою Рімана.
називається інтегральною сумою, або сумою Рімана.
Означення. Скінченна границя І суми s при 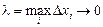 називається визначеним інтеграломвід функції f(x) на відрізку [a; b] і позначається
називається визначеним інтеграломвід функції f(x) на відрізку [a; b] і позначається
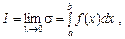 (1)
(1)
де а, b — відповідно нижня та верхня межі інтегрування, ò — знак інтеграла, введений Лейбніцем. (Лейбніц увів знак інтеграла ò як витягнуту букву S, що позначає підсумовування.) У разі існування границі І функція f(x) називається інтегровною на проміжку[a; b].
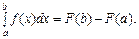 (2)
(2)
Це відома формула Ньютона—Лейбніца, яка поєднує диференціальне числення з інтегральним.
В інтегралі 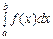 символ х позначає змінну інтегрування. Цю змінну можна позначати будь-якою іншою буквою, а отже, завжди маємо:
символ х позначає змінну інтегрування. Цю змінну можна позначати будь-якою іншою буквою, а отже, завжди маємо:
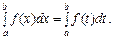
Зауважимо, що означення визначеного інтеграла можна застосувати лише до обмеженої функції.
Теорема. (Необхідна умова інтегрування.) Інтегровна на проміжку [a; b] функція обмежена.
| <== попередня сторінка | | | наступна сторінка ==> |
| Основні властивості невизначеного інтеграла | | | Властивості визначеного інтеграла |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |