Опис критерію

Якщо в методі χ² ми зіставляли частоти двох розподілів окремо по кожному розряду, то тут ми зіставляємо спочатку частоти по першому розряду, потім за сумою першого і другого розрядів, потім за сумою першого, другого і третього розрядів і т. д. Таким чином, ми зіставляємо всякий раз накопичені до даного розряду частоти.

Якщо відмінності між двома розподілами істотні, то в якийсь момент різниця накопичених частот досягне критичного значення, і ми зможемо визнати відмінності статистично достовірними. У формулу критерію λ включається ця різниця. Чим більше емпіричне значення λ, тим більш істотні відмінності.

Мал.1.10. Співставлення в критерію λ відмінностей між емпіричним та теоретичними накопиченими відносними частотами по кожному розряду

Обмеження критерію λ

1. Критерій вимагає, щоб вибірка була досить великою. При зіставленні двох емпіричних розподілів необхідно, щоб n₁,n₂ ≥ 50. Зіставлення емпіричного розподілу з теоретичним іноді допускається при n ≥ 5 (Ван дер Варден Б.Л., 1960; Гублера Є.В., 1978).

2. Розряди повинні бути впорядковані за зростанням або зменшенням якоїсь ознаки. Вони обов'язково повинні відображати якусь односпрямовану його зміну. Наприклад, ми можемо за розряди прийняти дні тижня, 1-й, 2-й, 3-й місяці після проходження курсу терапії, підвищення температури тіла, посилення почуття недостатності і т. д. У той же час, якщо ми візьмемо розряди, які випадково опинилися вибудованими в дану послідовність, то і накопичення частот буде відображати лише цей елемент випадкового сусідства розрядів.

Отже, ми не можемо накопичувати частоти за розрядами, які відрізняються лише якісно і не являють собою шкали порядку.

У всіх тих випадках, коли розряди є невпорядкованими за зростанням або спаданням якоїсь ознаки категорії, нам слід застосовувати метод χ².

АЛГОРИТМ 13 Розрахунок абсолютної величини різниці d між емпіричним і рівномірним розподілами 1. Занести в таблицю найменування розрядів і відповідні їм емпіричні частоти (перший стовпець). 2. Підрахувати відносні емпіричні частоти (частості) для кожного розряду за формулою: f⃰_емп=f_емп/n₁ де f⃰_емп – емпірична частота за даним розрядом; n – загальна кількість спостережень. Занести результати в другій стовпець. 3. Підрахувати накопичені емпіричні частості Ʃf^*_j за формулою: Ʃf^*_j= Ʃf^*_j_-₁ + f^*_j де Ʃf^*_j_-₁– частість, накопичена на попередніх розрядах; j – порядковий номер розряду; f^*_j– емпірична частість даного j-го розряду. Занести результати в третій стовпець таблиці. 4. Підрахувати накопичені теоретичні частості для кожного розряду за формулою: Ʃf^*_{Т j}= Ʃf^*_Тj-1 + f^*_{Т j} де Ʃf^*_Тj-1 – теоретична частість, накопичена на попередніх розрядах; j – порядковий номер розряду; f^*_{Т j} – теоретична частість даного розряду. Занести результати в третій стовпець таблиці. 5. Обчислити різниці між емпіричними і теоретичними накопиченими частостями за кожним розрядом (між значеннями 3-го і 4-го стовпців). 6. Записати в п'ятий стовпець абсолютні величини отриманих різниць, без їх знаку. Позначити їх як d. 7. Визначити за п'ятою колонкою найбільшу абсолютну величину різниці – d_max 8. За Табл. X визначити або розрахувати критичні значення d_max для даної кількості спостережень n. d_кр = 1,36/√n (p≤0,05) 1,63/√n (p≤0,01) Якщо d_max дорівнює критичному значенню d або перевищує його, відмінності між розподілами достовірні.

АЛГОРИТМ 14 Алгоритм розрахунку критерію λ при зіставленні двох емпіричних розподілів 1. Занести в таблицю найменування розрядів і відповідні їм емпіричні частоти, отримані в розподілі 1 (перший стовпчик) та в розподілі 2 (другий стовпчик). 2. Підрахувати емпіричні частоти по кожному розряду для розподілу 1 за формулою: f⃰_е=f_е/n₁ де f_е– емпірична частота в даному розряді; n₁ – кількість спостережень у вибірці. Занести емпіричні частоти розподілу 1 в третій стовпчик. 3. Підрахувати емпіричні частоти по кожному розряду для розподілу 2 за формулою: f⃰_е=f_е/n₂ де f_е– емпірична частота в даному розряді; n₂ – кількість спостережень у 2 вибірці. Занести емпіричні частоти розподілу 1 в четвертий стовпчик. 4. Підрахувати накопичені емпіричні частості для розподілу 1 за формулою: Ʃf⃰₁= Ʃf⃰і-₁+f⃰₁ де Ʃf⃰і-₁ – частість накопичення на попередніх розрядах; i – порядковий номер розряду; f⃰₁ – частість даного розряду. Отримані результати занести в п’ятий стовпчик. 5. Підрахувати накопичені емпіричні частості для розподілу 2 за тією ж формулою та записати результат в шостий стовпчик. 6. Підрахувати різницю між накопиченими частостями по кожному розряду. Записати в сьомий стовпчик абсолютні величини різниці, без їх знаку. Позначити їх як d. 7. Визначити за сьомим стовпчиком найбільшу абсолютну величину різниці d_max 8. Підрахувати значення критерію λ за формулою:

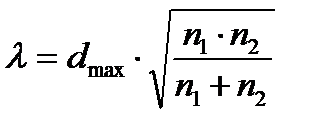де n1 – кількість спостережень в першій вибірці; n2 – кількість спостережень в другій вибірці. 9. За Табл. ХІ визначити, якому рівню статистичної значимості відповідає отримане значення λ. Якщо λ_емп≥1,36, відмінності між розподілами достовірні. λ_кр = 1,36 (р≤0,05) 1,63 (р≤0,01)

АЛГОРИТМ 15 Вибір критерію порівняння розподілів

1. Скільки рядів (с) має ознака?

с=2

с≥3

2. Які розподіли зіставляються

2. Яку шкалу представляють собою розряди

Емпіричне з теоретичним

2 емпіричних між собою

Номінативну: розряди відрізняються лише за якістю

Порядкову: розряди упорядкування за зростанням ознаки

При завданні вияву подібностей або відмінностей

При завданні вияву точки максимального накопичення відмінностей

n≤50

n˃50

Біноміальний критерій m

Критерій χ² з поправкою на неперервність

Критерій Фішера

Критерій χ² з поправкою на неперервність

Критерій χ²

Критерій λ Колмогорова-Смірнова

Критерій φ*–кутове перетворення Фішера

Призначення критерію φ*

Критерій Фішера призначений для зіставлення двох вибірок за частотою наявності ефекту, який цікавить дослідника.

<== попередня сторінка	\|	наступна сторінка ==>
Обмеження критерію	\|	Опис критерію

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.017 сек.