
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Принцип мінімаксу.
Розглянемо гру 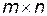 з матрицею
з матрицею 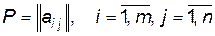 і визначимо найкращу серед стратегій
і визначимо найкращу серед стратегій 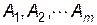 . Вибираючи стратегію
. Вибираючи стратегію 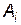 , гравець
, гравець  повинен розраховувати, що гравець
повинен розраховувати, що гравець  відповість на неї тією з стратегій
відповість на неї тією з стратегій 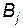 , для якої виграш для гравця
, для якої виграш для гравця  мінімальний (гравець
мінімальний (гравець  намагається перешкодити гравцю
намагається перешкодити гравцю  ). Позначимо через
). Позначимо через 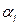 найменший виграш гравця
найменший виграш гравця  при виборі ним стратегії
при виборі ним стратегії 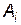 для всіх можливих стратегій гравця
для всіх можливих стратегій гравця  :
:
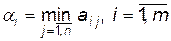
Серед чисел 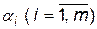 виберемо найбільше:
виберемо найбільше: 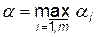 . Назвемо
. Назвемо 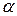 нижньою ціною гри, або максиміним виграшем (максиміном). Це гарантований виграш гравця
нижньою ціною гри, або максиміним виграшем (максиміном). Це гарантований виграш гравця  при будь-якій стратегії гравця
при будь-якій стратегії гравця  . Отже
. Отже
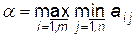
Стратегія, що відповідає максиміну, називається максиміною стратегією.
Гравець  зацікавлений в тому, щоб зменшити виграш
зацікавлений в тому, щоб зменшити виграш  . Вибираючи стратегію
. Вибираючи стратегію 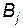 , він враховує максимально можливий виграш при цьому гравця
, він враховує максимально можливий виграш при цьому гравця  . Позначимо
. Позначимо
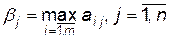
Серед чисел 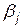 виберемо найменше
виберемо найменше 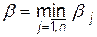 і назвемо
і назвемо 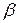 верхньою ціною гри або мінімаксним виграшем (мінімаксом). Це гарантований програш гравця
верхньою ціною гри або мінімаксним виграшем (мінімаксом). Це гарантований програш гравця  . Отже
. Отже
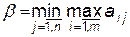
Стратегія, що відповідає мінімаксу, називається мінімаксною стратегією. Принцип, що диктує гравцям вибір найбільш «обережних» мінімаксних і максиміних стратегій, називається принципом мінімаксу.
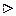 Визначимо верхню і нижню ціни гри і відповідні стратегії в прикладі 12.1, доповнивши таблицю рядком
Визначимо верхню і нижню ціни гри і відповідні стратегії в прикладі 12.1, доповнивши таблицю рядком 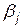 і стовпцем
і стовпцем 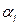 :
:
| стратегії | 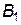
| 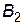
| 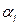
|
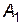
| -1 | -1 | |
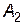
| -1 | -1 | |
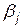
| 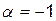
|
При виборі гравцем  стратегії
стратегії 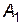 мінімальний виграш
мінімальний виграш 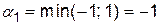 і відповідає стратегії
і відповідає стратегії 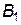 гравця
гравця  . При виборі стратегії
. При виборі стратегії 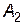 мінімальний виграш
мінімальний виграш 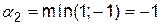 досягається при стратегії
досягається при стратегії 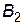 . Гарантуючи собі максимальний виграш при будь-якій стратегії гравця
. Гарантуючи собі максимальний виграш при будь-якій стратегії гравця  , тобто нижню ціну гри
, тобто нижню ціну гри 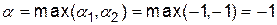 , гравець
, гравець  може вибрати будь-яку стратегію:
може вибрати будь-яку стратегію: 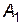 або
або 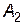 , тобто будь-яка стратегія є максиміною.
, тобто будь-яка стратегія є максиміною.
Вибираючи стратегію 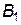 , гравець
, гравець  розуміє, що гравець
розуміє, що гравець  відповість стратегією
відповість стратегією 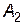 , щоб максимізувати свій виграш. Отже максимальний програш гравця
, щоб максимізувати свій виграш. Отже максимальний програш гравця  при виборі ним стратегії
при виборі ним стратегії 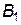 дорівнює
дорівнює 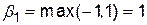 . Аналогічно
. Аналогічно 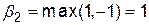 . Таким чином, при будь-якій стратегії гравця
. Таким чином, при будь-якій стратегії гравця  гарантований мінімальний програш гравця
гарантований мінімальний програш гравця  дорівнює
дорівнює 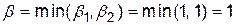 -- вершній ціні гри. В розглянутому прикладі верхня і нижня ціна гри різні:
-- вершній ціні гри. В розглянутому прикладі верхня і нижня ціна гри різні: 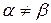 .
.
Якщо верхня і нижня ціни гри співпадає, то спільне значення верхньої і нижньої ціни гри 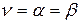 називається чистою ціною гри, або ціною гри. Мінімаксні стратегії, що відповідають ціні гри, являються оптимальними стратегіями, а їх сукупність – оптимальним розв’язком, або розв’язком гри. В цьому випадку гравець
називається чистою ціною гри, або ціною гри. Мінімаксні стратегії, що відповідають ціні гри, являються оптимальними стратегіями, а їх сукупність – оптимальним розв’язком, або розв’язком гри. В цьому випадку гравець  одержує максимальний гарантований (не залежний від поведінки гравця
одержує максимальний гарантований (не залежний від поведінки гравця  ) виграш
) виграш 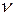 , а гравець
, а гравець  добивається мінімального гарантованого (не залежного від поведінки гравця
добивається мінімального гарантованого (не залежного від поведінки гравця  ) прогашу
) прогашу 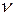 . Говорять, що розв’язок гри стійкий, тобто якщо один гравець притримується оптимальної стратегії, то для другого не може бути вигідним відхилятись від своєї оптимальної стратегії.
. Говорять, що розв’язок гри стійкий, тобто якщо один гравець притримується оптимальної стратегії, то для другого не може бути вигідним відхилятись від своєї оптимальної стратегії.
Пара чистих стратегій 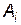 і
і 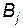 дає оптимальний розв’язок гри тоді і тільки тоді, коли відповідний їй елемент
дає оптимальний розв’язок гри тоді і тільки тоді, коли відповідний їй елемент 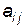 платіжної матриці є одночасно найбільшим в своєму стовпці і найменшим в рядку. Така ситуація, якщо вона існує, називається сідловою точкою.
платіжної матриці є одночасно найбільшим в своєму стовпці і найменшим в рядку. Така ситуація, якщо вона існує, називається сідловою точкою.
Позначимо 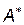 і
і 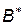 -- пару чистих стратегій, на яких досягається розв’язок гри в задачі з сідловою точкою. Введемо функцію виграшу першого гравця на кожній парі стратегій:
-- пару чистих стратегій, на яких досягається розв’язок гри в задачі з сідловою точкою. Введемо функцію виграшу першого гравця на кожній парі стратегій: 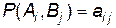 . Тоді з умов оптимальності в сідловій точці виконується подвійна нерівність:
. Тоді з умов оптимальності в сідловій точці виконується подвійна нерівність:
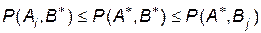 ,
,
яка справедлива для всіх 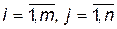 .
.
Дійсно, вибір стратегії 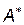 першим гравцем при оптимальній стратегії
першим гравцем при оптимальній стратегії 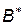 другого гравця максимізує мінімальний можливий виграш:
другого гравця максимізує мінімальний можливий виграш: 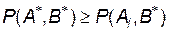 , а вибір стратегії
, а вибір стратегії 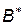 другим гравцем при оптимальній стратегії першого мінімізує максимальний програш:
другим гравцем при оптимальній стратегії першого мінімізує максимальний програш: 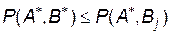 .
.
Приклад 12.2. Визначити нижню і верхню ціну гри, заданої платіжною матрицею:
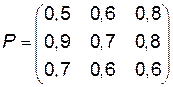
Чи має гра сідлову точку?
Розв’язок. Всі розрахунки проведемо в таблиці, до якої крім матриці 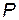 , введемо стовбець
, введемо стовбець 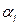 і рядок
і рядок 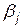 . Аналізуючи рядки матриці ( стратегії гравця
. Аналізуючи рядки матриці ( стратегії гравця  ), заповнимо стовбець
), заповнимо стовбець 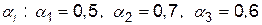 . Аналогічно по стовпцях :
. Аналогічно по стовпцях : 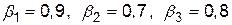 .
.
| стратегії | 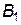
| 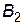
| 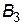
| 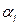
|
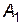
| 0,5 | 0,6 | 0,8 | 0,5 |
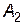
| 0,9 | 0,7 | 0,8 | 0,7 |
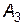
| 0,7 | 0,6 | 0,6 | 0,6 |
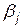
| 0,9 | 0,7 | 0,8 | 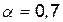 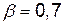
|
Нижня ціна гри 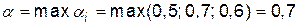 , а верхня ціна гри
, а верхня ціна гри 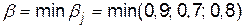 . Ці значення рівні:
. Ці значення рівні: 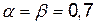 і досягаються на одній і тій же парі стратегій
і досягаються на одній і тій же парі стратегій 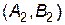 . Отже, гра має сідлову точку
. Отже, гра має сідлову точку 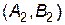 і ціна гри
і ціна гри 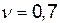 .
.
| <== попередня сторінка | | | наступна сторінка ==> |
| Платіжна матриця парної гри. | | | Розв’язування гри в мішаних стратегіях. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |