
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Види навантажень і основних деформацій
Основні гіпотези і припущення
Реальний об’єкт і розрахункова схема
Перед тим як починати розрахунки необхідно вияснити, що в даному випадку є головним, а що другорядним, тобто тим, що мало впливає на роботу системи в цілому. Другорядні фактори при розрахунках системи не враховуються.
Реальний об’єкт, звільнений від факторів, що мало впливають, називається розрахунковою схемою.
Для одного і того ж об’єкта може бути запропоновано декілька розрахункових схем в залежності від необхідної точності розрахунків і від того, яка сторона явища цікавить дослідника. Разом з тим одній і тій же розрахунковій схемі може відповідати багато різних реальних об’єктів, що дуже важливо, оскільки досліджуючи одну розрахункову схему, можна одержати рішення певного класу задач.
Вибір розрахункової схеми в опорі матеріалів починається із схематизації властивостей матеріалу, які називають гіпотезами.
Розглянемо основні гіпотези і припущення стосовно фізико-механічних властивостей матеріалів.
1. Гіпотеза про відсутність початкових внутрішніх зусиль.
Згідно з цією гіпотезою, припускають, що коли немає причин для деформації тіла (навантаження, зміна температури), то в усіх його точках внутрішні зусилля дорівнюють нулю. Тобто, сили взаємодії між частинками ненавантаженого тіла до уваги не беруть.
2. Гіпотеза про однорідність матеріалу. Фізико-механічні властивості тіла в різних точках можуть бути неоднаковими. В опорі матеріалів ці відмінності не враховують, припускаючи, що матеріал в усіх точках тіла має однакові властивості.
3. Гіпотеза про неперервність матеріалу. Згідно з цією гіпотезою, матеріал будь-якого тіла має неперервну будову і є суцільним середовищем. Припущення про неперервну будову дає змогу використовувати при розрахунках методи вищої математики.
4. Гіпотеза про ізотропність матеріалу. Ця гіпотеза передбачає, що матеріал тіла має однакові властивості в усіх напрямках. Багато матеріалів складається з кристалів, в яких фізико-механічні властивості в різних напрямках істотно відрізняються. Проте, завдяки наявності в тілі великої кількості безладно розміщених кристалів, властивості всього тіла в різних напрямках вирівнюються.
Припущення про ізотропність добре підтверджується практикою для більшості матеріалів і лише наближено для таких матеріалів, як камінь, пластмаси, залізобетон. Матеріали, які мають неоднакові властивості в різних напрямках, називають анізотропними.
5. Гіпотеза про ідеальну пружність. Ця гіпотеза передбачає, що в певних межах навантаження матеріал виявляє ідеальну пружність, тобто після зняття навантаження деформації повністю зникають.
Розглянемо тепер гіпотези, пов’язані з деформаціями елементів конструкцій. Зміну лінійних і кутових розмірів тіла називають відповідно лінійною і кутовою деформаціями. Зміну положення (координат) точок тіла, спричинену деформацією, називають переміщенням.
6. Гіпотеза про малість деформацій. За цим припущенням деформації тіла і пов’язані з ними переміщення точок і перерізів дуже малі порівняно з розмірами тіла. На підставі цього змінами в розміщенні зовнішніх сил, спричинених деформацією, нехтують.
7. Гіпотеза про лінійну залежність між навантаженням і деформацією. Згідно з цією гіпотезою, зміщення точок і перерізів пружного тіла в певних межах навантаження прямо пропорційне силам, які спричиняють ці переміщення.
8. Гіпотеза плоских перерізів, або гіпотеза Бернулі. Згідно з цією гіпотезою, плоскі поперечні перерізи, зроблені в тілі до деформації, залишаються під час деформації плоскими і нормальними до осі.
|

У процесі роботи машин і споруд їх вузли і деталі сприймають і передають різні навантаження, тобто силові дії, які спричиняють зміну внутрішніх сил і деформації вузлів і деталей. Сили бувають масові або об’ємні (сили тяжіння, сили інерції), або поверхневі, які зумовлені контактною взаємодією розглядуваного елемента з сусідніми елементами або прилеглим до нього середовищем (наприклад, пара, повітря, рідина).
З теоретичної механіки відомо, що поверхневі навантаження бувають зосередженими або розподіленими. Залежно від характеру дії навантаження поділяють на статичні і динамічні.
Динамічними називають навантаження, значення яких, напрям або місце прикладання швидко змінюються з часом. До динамічних належать ударні, раптово прикладені і повторно-змінні навантаження. Ударні навантаження виникають, наприклад, під час кування металу або забивання паль; прикладом раптово прикладеного навантаження є тиск колеса, яке котиться по рейці; повторно-змінних навантажень зазнають, наприклад, деталі кривошипно-повзунного механізму двигуна.
Треба пам’ятати, що до зовнішніх сил, які беруть до уваги при розрахунках конструкцій, належать не тільки активні сили, а й реакції опор і сили інерції.
Перейдемо до розгляду питання про основні деформації. Під дією зовнішніх сил тіло деформується, тобто його точки змінюють своє положення в просторі. Проекції вектора переміщення на осі вибраної системи координат позначаються U, V, W відповідно осям x, y, z. Крім лінійних є кутові переміщення: відрізок прямої між двома близькими точками в результаті дії зовнішніх сил не тільки міняє свої розміри, а повертається в просторі на деякий кут.
При визначенні деформації в околі довільної точки А (рисунок 1.1, а) розглядають малий відрізок АВ довжиною l, проведений через цю точку в довільному напрямку. В результаті деформації відрізок АВ переміститься і поміняє свою довжину на Dl, тоді відношення
 (1.1)
(1.1)
називається відносною лінійною деформацією в точці А, в напрямку АВ. В тій же точці, в іншому напрямку деформація буде іншою. Якщо розглядають деформації в напрям координатних осей x, y, z то їх позначають відповідно 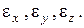
Крім лінійних деформацій мають місце також кутові деформації (рисунок 1.1, б). Кутова деформація - це величина зміни прямого кута в процесі деформування між двома перпендикулярними до деформації прямими, проведеними через точку А. Вона називається деформацією зсуву. В координатних площинах деформації зсуву позначають 
Сукупність лінійних та кутових деформацій в різних напрямках і в різних площинах, які проходять через розглядувану точку середовища, визначають деформований стан в точці.
Читайте також:
- II. Критерій найбільших лінійних деформацій
- R – розрахунковий опір грунту основи, це такий тиск, при якому глибина зон пластичних деформацій (t) рівна 1/4b.
- АДАПТАЦІЯ ОПОРНО-РУХОВОГО АПАРАТУ ТА ФУНКЦІОНАЛЬНИХ СИСТЕМ ОРГАНІЗМУ ДО ФІЗИЧНИХ НАВАНТАЖЕНЬ
- Амортизація основних засобів
- Амортизація основних засобів, основні методи амортизації
- Амортизація основних засобів.
- Амортизація основних фондів
- Амортизація основних фондів
- Амортизація основних фондів підприємства. Методи нарахування амортизації
- Амортизація основних фондів підприємства. Методи нарахування амортизації.
- Амортизація основних фондів, методи її нарахування.
- Аналіз ефективності використання основних засобів.
| <== попередня сторінка | | | наступна сторінка ==> |
| Предмет і задачі курсу | | | Внутрішні сили. Метод перерізів |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |