
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Координатами.
Нехай в системі координат ХОУ задані  і
і  . Тоді:
. Тоді:
1. 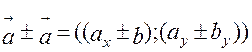 Координати суми (різниці) двох векторів дорівнює сумі (різниці) однойменних координат цих векторів.
Координати суми (різниці) двох векторів дорівнює сумі (різниці) однойменних координат цих векторів.
2. 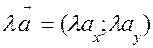 При множенні вектора на число, на це число перемножують його координати.
При множенні вектора на число, на це число перемножують його координати.
3. 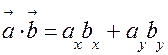 Скалярний добуток двох векторів дорівнює сумі добутків однойменних координат.
Скалярний добуток двох векторів дорівнює сумі добутків однойменних координат.
4. 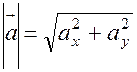 Модуль вектора дорівнює кореневі квадратному із суми квадратів його координат.
Модуль вектора дорівнює кореневі квадратному із суми квадратів його координат.
5. 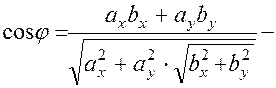 формула кута між двома векторами.
формула кута між двома векторами.
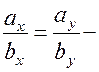 умови колінеарності векторів. Заданих своїми векторами.
умови колінеарності векторів. Заданих своїми векторами.
9. Векторний добуток векторів.
Векторним добутком вектора  на не колінеарний вектор
на не колінеарний вектор  називається такий вектор
називається такий вектор  , який задовольняє наступні вимоги:
, який задовольняє наступні вимоги:
1. Вектор  перпендикулярний вектору
перпендикулярний вектору  і вектору
і вектору  , тобто площині, яка містить вектори
, тобто площині, яка містить вектори  і
і  ;
;
2. Довжина вектора  чисельно дорівнює площі паралелограма, побудованого на векторах
чисельно дорівнює площі паралелограма, побудованого на векторах  і
і  як на сторонах
як на сторонах 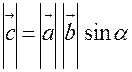 .
.
3. Орієнтація векторів  ,
,  ,
,  співпадає з орієнтацією векторів
співпадає з орієнтацією векторів
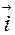 ,
,  ,
,  ( права трійка).
( права трійка).
Властивості:
1.  ; 3.
; 3.  ;
;
2.  ; 4. Якщо
; 4. Якщо 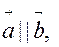 то
то 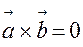 .
.
Якщо  , то:
, то:
 формула векторного добутку
формула векторного добутку
векторів, заданих своїми координатами.
10. Відстань між двома точками. Ділення
відрізка в заданому відношенні і навпіл.
Якщо  то
то  ,
,
або  Якщо
Якщо  і
і  , де
, де 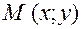 , то
, то 
 . Якщо точка М ділить відрізок АВ, то
. Якщо точка М ділить відрізок АВ, то 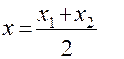
 .
.
11. Пряма лінія на площині.
1. Рівняння  називається канонічним, або рівнянням прямої, що проходить через точку з заданим направляючим вектором.
називається канонічним, або рівнянням прямої, що проходить через точку з заданим направляючим вектором.
2. Рівняння  називається параметричним рівнянням прямої.
називається параметричним рівнянням прямої.
3. 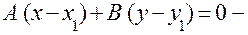 рівняння прямої, що проходить через задану точку з заданим нормальним вектором.
рівняння прямої, що проходить через задану точку з заданим нормальним вектором.
4. Рівняння 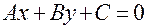 в прямокутній системі координат визначає пряму і причому єдину ( загальне рівняння прямої).
в прямокутній системі координат визначає пряму і причому єдину ( загальне рівняння прямої).
5. Частинні випадки загального рівняння прямої:  ( через початок координат);
( через початок координат); 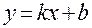 ( з кутовим коефіцієнтом і початковою координатою).
( з кутовим коефіцієнтом і початковою координатою).
6. 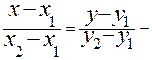 рівняння прямої, що проходить через дві точки.
рівняння прямої, що проходить через дві точки.
7. 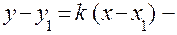 рівняння прямої, що проходить через задану точку з заданим кутовим коефіцієнтом (рівняння пучка прямих).
рівняння прямої, що проходить через задану точку з заданим кутовим коефіцієнтом (рівняння пучка прямих).
8.  формула кута між двома перетинаючими прямими.
формула кута між двома перетинаючими прямими.
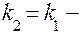 умова паралельності прямих,
умова паралельності прямих,
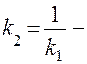 умова перпендикулярності прямих.
умова перпендикулярності прямих.
12. Криві другого порядку.
1. Коло.
Множина всіх точок площини, однаково віддалених від даної точки ( центра) називається колом.
 рівняння кола, з центром в точці
рівняння кола, з центром в точці 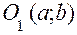 і радіусом R.
і радіусом R.
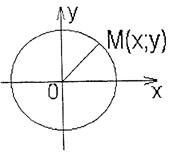
2. Еліпс.
Еліпсом називається множина всіх точок площини, сума відстаней від кожної із яких до двох заданих точок, які називаються фокусами, є величина постійна, більша, ніж відстань між фокусами.
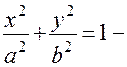 канонічне рівняння еліпса, 2а – велика вісь еліпса;
канонічне рівняння еліпса, 2а – велика вісь еліпса; 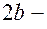 мала вісь еліпса; 2с – фокусна відстань;
мала вісь еліпса; 2с – фокусна відстань;  зв’язок між елементами а, b і с.
зв’язок між елементами а, b і с.  ексценрисітет еліпса.
ексценрисітет еліпса.

3. Гіпербола.
Гіперболою називається множина всіх точок площини, модуль різниці відстаней від кожної з яких до двох заданих точок, які називаються фокусами, є величина постійна, менша, ніж фокусна відстань.
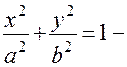 канонічне рівняння гіперболи, 2а – дійсна вісь;
канонічне рівняння гіперболи, 2а – дійсна вісь;
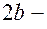 уявна вісь;
уявна вісь; 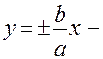 рівняння асимптот;
рівняння асимптот; 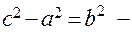 зв’язок між елементами а, b і с. Якщо
зв’язок між елементами а, b і с. Якщо 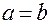 , то гіпербола називається рівносторонньою і її рівняння
, то гіпербола називається рівносторонньою і її рівняння  .
.

4. Парабола.
Параболою називається множина всіх точок площини, кожна з яких однаково віддалена від точки, яка називається фокусом і від прямої, яка називається директрисою.
 канонічне рівняння параболи, р – параметр параболи ( це відстань від фокуса до директриси.)
канонічне рівняння параболи, р – параметр параболи ( це відстань від фокуса до директриси.)

13. Рівняння прямої і площини в просторі.
1. Рівняння прямої в просторі.
 канонічне рівняння прямої в просторі, або рівняння прямої, що проходить через задану точку з заданим направляючим вектором.
канонічне рівняння прямої в просторі, або рівняння прямої, що проходить через задану точку з заданим направляючим вектором.

 параметричне рівняння прямої.
параметричне рівняння прямої.
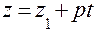
 рівняння прямої, що проходить через дві точки.
рівняння прямої, що проходить через дві точки.
 умова перпендикулярності прямих.
умова перпендикулярності прямих.
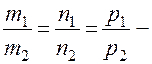 умова паралельності прямих.
умова паралельності прямих.
 умова того, що прямі лежать в одній площині.
умова того, що прямі лежать в одній площині.
 Формула конуса кута між двома перетинаючи ми прямими.
Формула конуса кута між двома перетинаючи ми прямими.
1. Рівняння площини.
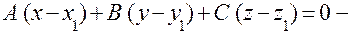 рівняння площини, що проходить через задану точку з заданим нормальним вектором.
рівняння площини, що проходить через задану точку з заданим нормальним вектором.
Якщо в загальному рівнянні площини відсутній член з якою-небудь змінною, то площина паралельна відповідній вісі координат.
Якщо в загальному рівнянні площини два коефіцієнти при змінних дорівнюють нулю, то площина паралельна відповідній координатній площині.
 рівняння площини, що проходить через три точки.
рівняння площини, що проходить через три точки.
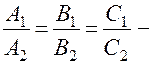 умова паралельності площини.
умова паралельності площини.
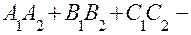 умова перпендикулярності площин.
умова перпендикулярності площин.
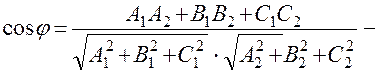 формула косинуса кута між двома площинами.
формула косинуса кута між двома площинами.
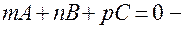 умова паралельності прямої і площини.
умова паралельності прямої і площини.
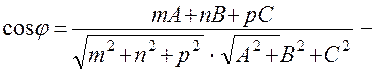 формула синуса кута між прямою і площиною.
формула синуса кута між прямою і площиною.
| <== попередня сторінка | | | наступна сторінка ==> |
| Тема №6. Вектори та координати | | | Лист контролю. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |