
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Лист контролю.
Модуль №6.
1. Поняття вектора.
2. Лінійні операції над векторами.
3. Базис і координати. Прямокутні координати на площині та в просторі.
4. Координати вектора.
5. Дії над векторами в координатній формі.
6. Умова колінеарність векторів.
7. Скалярний добуток векторів.
8. Умова перпендикулярності векторів.
9. Кут між векторами.
10. Відстань між двома точками.
11. Ділення відрізка в заданому відношенні.
12. Векторний добуток векторів.
13. Пряма на площині і її рівняння. Загальне рівняння прямої і його дослідження. Канонічне рівняння прямої, нормальне рівняння прямої. Кут між прямими.
14. Криві другого порядку. Коло. Еліпс. Гіпербола. Парабола.
15. Рівняння прямої в просторі.
16. Рівняння площини, яка задана точкою і нормальним вектором.
Література:
1. О.М. Афанасьєва «Математика» . 2001р.
2. О.М. Афанасьєва «Дидактичні матеріали з математики». 2001р.
3. О.В. Погорєлова «Геометрія» . 10 – 11 кл. 1995р.
4. Н.Г. Федін «Геометрія». 1989р.
5. Н.В. Богомолов «Практические занятия по математике». 1990г.
Тема №7 : Інтеграл та його застосування.
1. Неозначений інтеграл та його застосування.
2. Таблиця основних інтегралів.
3. Методи інтегрування.
4. Означений інтеграл.
5. Геометричний зміст означеного інтеграла.
6. Основні властивості означеного інтеграла.
7. Формула Ньютона – Лейбніца.
8. Застосування означеного інтеграла.
1. Неозначений інтеграл та його застосування.
Означення. Функція 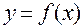 , визначена на множині х називається первісною для
, визначена на множині х називається первісною для  , визначеною на цій же множині х, якщо для всіх із цієї множини
, визначеною на цій же множині х, якщо для всіх із цієї множини 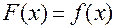 , або
, або 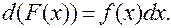
Теорема. Якщо функція  являється первісною для
являється первісною для  на деякій множині х, то функція
на деякій множині х, то функція 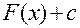 також являється первісною для
також являється первісною для  на множині х.
на множині х.
Означення. Сукупність первісних 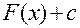 для
для  , означених на множині х називається неозначеним інтегралом від функції
, означених на множині х називається неозначеним інтегралом від функції  на множині х і позначається:
на множині х і позначається:
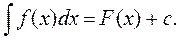
 підінтегральна функція.
підінтегральна функція.
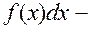 підінтегральний вираз.
підінтегральний вираз.
с – постійна інтегрування.
Властивості неозначеного інтеграла.
1. Похідна від неозначеного інтеграла дорівнює підінтегральній функції 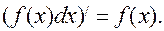
2. Диференціал від неозначеного інтеграла дорівнює підінтегральному виразу 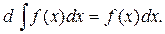
3. Постійний множник можна виносити за знак інтеграла 
4. Неозначений інтеграл від алгебраїчної суми двох неперервних функцій дорівнює алгебраїчній сумі інтегралів від кожної з цих функцій 
2. Таблиця основних інтегралів.
1. 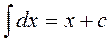 14.
14. 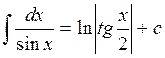
2. 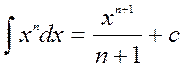 15.
15. 
3. 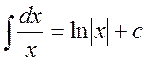 16.
16. 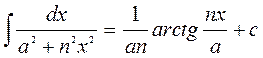
4.  17.
17. 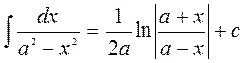
5.  18.
18. 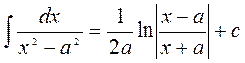
6.  19.
19. 
7.  20.
20. 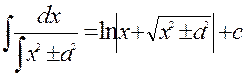
8. 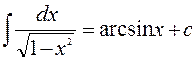 21.
21. 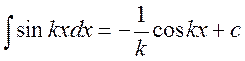
9.  22.
22. 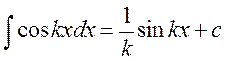
10. 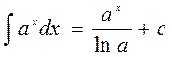 23.
23. 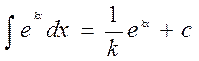
11. 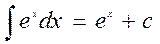 24.
24. 
12. 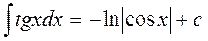 25.
25. 
13. 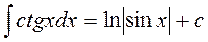
3. Методи інтегрування.
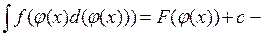 метод підстановки.
метод підстановки.
 формула інтегрування за частинами.
формула інтегрування за частинами.
4. Визначений інтеграл.
Нехай 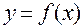 неперервна на
неперервна на  . Якщо існує границя послідовності інтегральних сум, одна і таж, незалежно від вибору точки
. Якщо існує границя послідовності інтегральних сум, одна і таж, незалежно від вибору точки 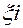 , то
, то  називається інтегральною, границя називається означеним інтегралом і позначається
називається інтегральною, границя називається означеним інтегралом і позначається 

а – нижня межа інтегрування;
b – верхня межа інтегрування;
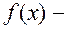 підінтегральна функція;
підінтегральна функція;
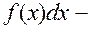 підінтегральний вираз.
підінтегральний вираз.
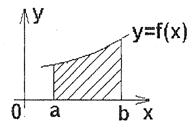
5. Геометричний зміст визначеного інтеграла.
Якщо інтегрована на  функція
функція  невід’ємна, то означений інтеграл
невід’ємна, то означений інтеграл  чисельно дорівнює площі S криволінійної трапеції, обмеженої графіком функції
чисельно дорівнює площі S криволінійної трапеції, обмеженої графіком функції  , віссю ОХ і прямими х=а і х=b.
, віссю ОХ і прямими х=а і х=b.
6. Основні властивості визначеного інтеграла.
1. Постійний множник можна виносити за знак інтеграла  ;
;
2. Означений інтеграл від алгебраїчної суми двох неперервних функцій дорівнює алгебраїчній сумі їх інтегралів 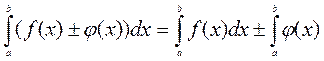 ;
;
3. Якщо a < c < b, то 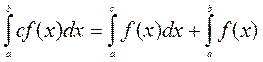 ;
;
4. Якщо функція  на
на  , де a < b, то
, де a < b, то  ;
;
5. Якщо 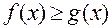 для
для 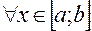 , то
, то  ;
;
Якщо т і М – найменше і найбільше значення функції  ;
;
6. на  , де a < b, то
, де a < b, то 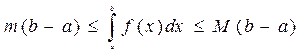 ;
;
7. Теорема про середнє.
Якщо функція  неперервна на
неперервна на  , то існує точка
, то існує точка 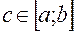 така, що
така, що 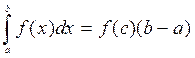 ;
;
8. 
7. Формула Ньютона – Лейбніца.
Якщо функція  неперервна на проміжку
неперервна на проміжку  , а
, а  являється якою-небудь її первісною на цьому проміжку, то
являється якою-небудь її первісною на цьому проміжку, то 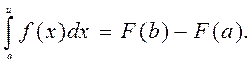
Формула Ньютона – Лейбніца записується в вигляді:  і показує, що значення інтеграла дорівнює різниці значень первісної підінтегральної функції. Таким чином: щоб обчислити інтеграл
і показує, що значення інтеграла дорівнює різниці значень первісної підінтегральної функції. Таким чином: щоб обчислити інтеграл  , необхідно:
, необхідно:
1. Знайти неозначений інтеграл від функції  .
.
2. В отриманий вираз підставити замість х спочатку верхню межу b, потім нижню межу а, і з першого результату віднити другий.
8. Застосування визначеного інтегралу.
1. Обчислення площ плоских фігур. 
Обчислення об’ємів.
а) 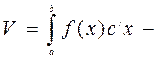 за площею поперечного перерізу;
за площею поперечного перерізу;
2. б) 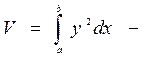 об’єм тіла, утвореного обертанням навколо вісі ОХ;
об’єм тіла, утвореного обертанням навколо вісі ОХ;
в)  об’єм тіла, утвореного обертанням навколо вісі OY;
об’єм тіла, утвореного обертанням навколо вісі OY;
3. Довжина дуги кривої  ;
;
4. Площа поверхні обертання 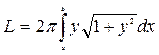 ;
;
5. Робота змінної сили  ;
;
6. Обчислення маси стержня змінної густини 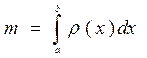 ;
;
7. Обчислення статистичних моментів і центра мас плоскої кривої 

Читайте також:
- D) оснащення виробництва обладнанням, пристроями, інструментом, засобами контролю.
- IV. Питання самоконтролю.
- Види і форми контролю.
- Види і форми контролю.
- Види контролю.
- Види управлінського контролю.
- Види, форми і методи фінансового контролю.
- Визначення та необхідність контролю.
- Відповідальність посадових осіб органів державного фінансового контролю.
- Вплив експериментатора на результати дослідження. Способи контролю.
- Завдання, функції і види педагогічного контролю.
- Захист прав суб'єктів господарювання при порушенні порядку здійснення господарського контролю.
| <== попередня сторінка | | | наступна сторінка ==> |
| Координатами. | | | Двогранний кут. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |