
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Тема №6. Вектори та координати
Лист контролю.
Модуль №5.
1. Початкові поняття стереометрії.
2. Аксіоми стереометрії та наслідки з них.
3. Взаємне розміщення прямих в просторі.
4. Взаємне розміщення прямої і площини в просторі.
5. Взаємне розміщення площин в просторі.
6. Паралельне проектування та його властивості.
7. Перпендикулярність прямої і площини.
8. Зв’язок між паралельністю і перпендикулярністю прямих і площин.
9. Теорема про три перпендикуляри.
10. Кут між прямою і площиною.
11. Двогранний кут. Лінійний кут двогранного кута.
12. Перпендикулярність площин.
Література:
1. О.М. Афанасьєва «Математика» . 2001р.
2. О.М. Афанасьєва «Дидактичні матеріали з математики». 2001р.
3. О.В. Погорєлов «Геометрія». 10 – 11 кл. 1995р.
4. Н.Г. Федін «Геометрія». 1989р.
1. Скалярні та векторні величини.
2. Лінійні операції над векторами.
3. Теорема про колінеарні вектори.
4. Розкладання вектора на два скалярні неколінеарні вектори.
5. Векторний базис на площині і в просторі. Система координат на площині і в просторі.
6. Полярні координати.
7. Скалярний добуток векторів.
8. Операції над векторами заданими своїми координатами.
9. Векторний добуток векторів.
10. Відстань між двома точками. Ділення відрізка в заданому відношенні  і навпіл.
і навпіл.
11. Пряма лінія на площині.
12. Криві другого порядку.
13. Рівняння прямої і площини в просторі
1. Скалярні та векторні величини.
Скалярна величина – це величина, для визначення якої треба знати тільки число.
Векторна величина – вказує напрямок і числове значення.
Вектор – це направлений відрізок 
Вектор, початок і кінець якого співпадають, називається нульовим вектором.
Довжина вектора, називається його модулем  .
.
Два вектори називаються рівними, якщо виконуються умови:
1) Вектори лежать на паралельних прямих;
2) Вектори спів паралельні;
3) Вектори мають рівні модулі.
Два вектори називаються колінеарними, якщо вони лежать на паралельних прямих.
2. Лінійні операції над векторами.
1). Сума векторів.
Сумою двох векторів називається вектор, який сполучає початок першого і кінець другого векторів при умові, що другий вектор виходить із кінця першого.
Властивості:
1)  ; 3)
; 3) 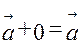
2)  ; 4)
; 4) 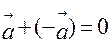
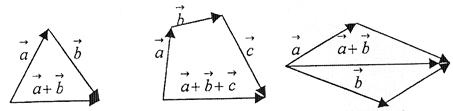
правило правило правило
трикутника многокутника паралелограма
2). Різниця векторів.
Різницею векторів, які виходять з однієї точки називається вектор, який сполучає кінці цих векторів і направлений в сторону того вектора, з якого віднімаємо.
3). Добуток векторів на скаляр.
Добуток  на скаляр
на скаляр 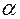 називається вектор
називається вектор  , який задовольняє наступні вимоги:
, який задовольняє наступні вимоги:
1) 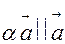
2) 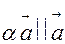 , якщо
, якщо 
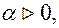
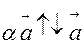 , якщо
, якщо 
3) 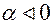
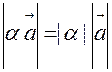
3. Теорема про колінеарні вектори.
Якщо вектори колінеарні, то існує число  перемноживши на яке один із векторів, отримаємо другий вектор
перемноживши на яке один із векторів, отримаємо другий вектор  , якщо
, якщо  .
.
4. Розкладання вектора на два складові
неколінеарні вектори.
Розкласти вектор на два складові не колінеарні вектори – це значить представити його у вигляді суми двох векторів, колінеарних складовим.

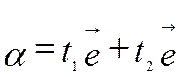
5. Векторний базис на площині і в просторі.
Система координат на площині і в просторі.
Сукупність фіксованої точки О і ортонормованого базиса 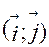
називається фіксованою декартовою системою координат на площині.

 - радіус – вектор точки М.
- радіус – вектор точки М.
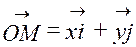 ;
;  координати
координати
радіус – вектор.
Сукупність фіксованої точки О і ортонормованого базиса 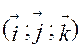 називається прямокутною декартовою системою координат в просторі.
називається прямокутною декартовою системою координат в просторі.


Якщо  , то
, то  координати вектора дорівнюють різниці відповідних координат кінцевої і початкової точки.
координати вектора дорівнюють різниці відповідних координат кінцевої і початкової точки.
6. Полярні координати.
Сукупність точки О, прометея ОР і одиничного вектора 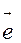 називається полярною системою координат.
називається полярною системою координат.

О – полюс, ОР – полярна вісь.
r – полярний радіус,  полярний кут.
полярний кут.
r і  полярні координати точки М.
полярні координати точки М.
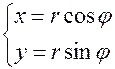
Зв’язок між прямокутниками і полярними координатами.
7. Скалярний добуток векторів.
Скалярним добутком векторів називається добуток їх модулів на косинус кута між ними 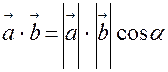
Властивості:
1) 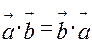 ;
;
2) 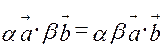 ;
;
3) 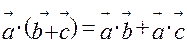 ;
;
4)  ;
;
5) 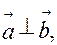

8. Операції над векторами заданими своїми
Читайте також:
- Білково-експресуючі вектори
- Вантажообіг і координати магазинів, які обслуговуються
- Вектори зовнішньої політики США
- Вектори кутової швидкості і кутового прискорення.
- Вектори рівні, якщо вони колінеарні, мають однакові напрями і рівні модулі.
- Вектори, лінійні операції над векторами
- Визначення скалярного добутку через координати.
- Вираження мішаного добутку через координати векторів.
- Власні числа та власні вектори матриці
- Е) Власні вектори і власні значення лінійного перетворення
- Приклад. Перевірити, чи є ортогональними вектори
- Приклад. Перевірити, чи є ортогональними вектори
| <== попередня сторінка | | | наступна сторінка ==> |
| Лист контролю. | | | Координатами. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |