• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Лист контролю.

Модуль №8, 9.

1. Многогранники.

2. Призма. Паралелепіпед.

3. Правильні многогранники.

4. Піраміда. Зрізана піраміда.

5. Властивості зрізаної піраміди.

6. Поняття об’єму тіла.

7. Об’єм тіла по площі поперечного перерізу.

8. Площа поверхні та об’єм призми.

9. Площа поверхні та об’єм піраміди.

10. Площа поверхні та об’єм зрізаної піраміди.

11. Циліндр. Площа поверхні та об’єм циліндра.

12. Конус. Площа поверхні та об’єм конуса.

13. Зрізаний конус. Площа поверхні та об’єм зрізаного конуса.

14. Сфера. Рівняння сфери.

15. Площа поверхні сфери.

16. Куля. Об’єм кулі.

Література:

1. О.М. Афанасьєва «Математика». 2001р.

2. О.М. Афанасьєва «Дидактичні матеріали з математики». 2001р.

3. О.В. Погорєлов «Геометрія» 10 – 11 кл. 1995р.

4. Н.Г. Федін «Геометрія». 1989р.

Тема №10: Теорія імовірності.

1. Означення імовірності.

2. Класифікація подій.

3. Алгебра подій.

4. Означення імовірності подій.

5. Теореми додавання імовірності.

6. Теореми множення імовірності.

7. Формула повної імовірності.

8. Формула Бейєса.

9. Незалежні випробування. Схема Бернулі.

10. Поняття про статистичну імовірність. Закон великих чисел.

11. Дискретні випадкові величини.

12. Числові характеристики випадкової величини.

13. Предмет і основні задачі математичної статистики.

1. означення імовірності.

Теорія імовірності – це математична дисципліна, яка вивчає закономірності масових випадкових явищ.

Основним поняттям теорії імовірності є подія A,B,C,D,U,V…

2. Класифікація подій.

Події поділяються на:

1. Випадкові (A,B,C,D). Подія А називається випадковою, якщо в даному випробуванні вона може відбуватися, а може і не відбутися.

2. Вірогідно (U). Подія U називається вірогідною, якщо в даному випробуванні вона обов’язково відбувається.

3. Неможливо (V). Подія V називається неможливою, якщо в даному випробуванні вона відбутися не може.

В свою чергу випадкові події поділяються на:

1. Сумісні і несумісні події.

Дві події називаються сумісними, якщо в даному випробуванні вони можуть виконуватись одночасно.

2. Залежні і незалежні події.

Дві події називаються незалежними, якщо в даному випробуванні результат однієї з них не впливає на результат іншої події.

3. Протилежні події.

Дві події називаються протилежними, якщо одна і лише одна з них обов’язково здійснюється в даному випробуванні.

4. Повна група подій.

Сукупність подій утворюють повну групу подій, якщо виконуються дві умови:

1) принаймні одна з цих подій виконується;

2) події попарно несумісні.

3. Алгебра подій.

Сумою подій А і В називається подія С, яка полягає у здійсненні при даному випробуванні або події А, або події В, або обох разом А+В=С.

Властивості:

1. ;

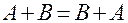2. ;

3. ;

4. ;

5. .

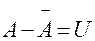Суму подій можна записати так:

Добутком двох подій А і В називається подія С, яка полягає в здійсненні під час випробуванні і події А, і події В.

Властивості:

1. ;

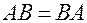2. ;

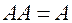3. ;

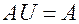4. ;

5.

4. Означення імовірності події.

Означення:

Імовірністю випадкової події називається відношення кількості подій, які сприяють цій події до кількості всіх можливих, рівно можливих і попарно несумісних елементарних подій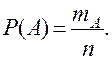

5. Теореми додавання ймовірностей.

Теорема 1. Імовірність суми двох несумісних подій дорівнює сумі ймовірностей цих подій.

Наслідок 1. Сума ймовірностей протилежних подій дорівнює одиниці.

Наслідок 2. Імовірність суми подій, які складають повну групу подій дорівнює одиниці.

Теорема 2. Імовірність суми двох сумісних подій дорівнює сумі ймовірностей цих подій без імовірності їх добутку.

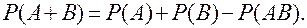
6. Теорема множення ймовірностей.

Теорема 3. Імовірність добутку двох незалежних подій дорівнює добутку ймовірностей цих подій.

Умова імовірності події:

Якщо події А і В залежні, то імовірність другої події залежить від результату здійснення першої події і це записується так: 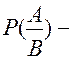називається умовною імовірністю і читається: імовірність події А при умові, що здійснюється подія В.

Теорема 4. Імовірність добутку двох залежних подій дорівнює добутку імовірності однієї з цих подій на умовну імовірність другої події.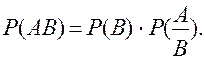

7. Формула повної імовірності.

Нехай події утворюють повну групу подій і подія А здійснюється з однією з цих подій 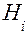з умовою імовірності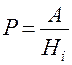

Знайти імовірність події А.

Якщо - повна група подій, то

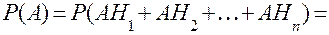
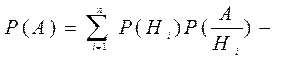формула повної імовірності.

8. Формула Бейєса.

Нехай подія А здійснюється. Яка імовірність того, що подія А здійснюється з подією .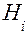

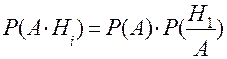
9. Незалежні випробування. Схема Бернулі.

Взаємно незалежними називаються такі випробування, в яких імовірність результату кожного із них не залежить від того, які результати матиме решта випробування.

Нехай відбувається n незалежних випробувань, у кожного з яких подія А може наступити, чи не наступити. Імовірність здійснення події А в кожному випробуванні однакова і дорівнює 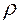, а імовірність не здійснення події А є

Знайти імовірність того, що подія А настане k разів.

Задача такого типу називається схемою Бернулі.

формула Бернулі.

10. Поняття про статистичну імовірність.

Читайте також:

1. D) оснащення виробництва обладнанням, пристроями, інструментом, засобами контролю.
2. IV. Питання самоконтролю.
3. Види і форми контролю.
4. Види і форми контролю.
5. Види контролю.
6. Види управлінського контролю.
7. Види, форми і методи фінансового контролю.
8. Визначення та необхідність контролю.
9. Відповідальність посадових осіб органів державного фінансового контролю.
10. Вплив експериментатора на результати дослідження. Способи контролю.
11. Завдання, функції і види педагогічного контролю.
12. Захист прав суб'єктів господарювання при порушенні порядку здійснення господарського контролю.

Переглядів: 568