• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Теоретичні відомості

Якщо між економічними явищами існують нелінійні співвідношення, то вони виражаються за допомогою відповідних нелінійних функцій.

Наприклад, нелінійними виявляються виробничі функції (залежності між обсягом виготовленої продукції і основними факторами виробництва - працею, капіталом і т.п.), функції попиту (залежність між попитом на товари або послуги і їхні ціни, або доходом) та інше.

Для оцінки параметрів нелінійних моделей використовують два підходи. Перший підхід заснований на лінеаризації моделі і полягає в тому, що за допомогою перетворень вихідних змінних залежність, яку досліджують, представляють у вигляді лінійного співвідношення між перетвореними змінними.

Другий підхід звичайно застосовують у випадку, коли підібрати відповідне перетворення, що лінеаризує, не вдається. У цьому випадку застосовують методи нелінійної оптимізації на основі вихідних змінних. Для лінеаризації моделі в рамках першого підходу можуть використовуватися як моделі, нелінійні за змінними, так і нелінійні за параметрами. Якщо модель нелінійна за змінними, то введенням нових змінних її можна звести до лінійної моделі, для оцінки параметрів якої використати звичайний метод найменших квадратів. Треба, однак, відзначити й недолік такої заміни змінних, пов'язаний з тим, що оцінки параметрів виходять не з умови мінімізації суми квадратів відхилень для вихідних змінних, а з умови мінімізації суми квадратів відхилень для перетворених змінних, що не те саме. У зв'язку із цим необхідне певне уточнення отриманих оцінок.

Економічна практика вже накопичила певний досвід і певні типи кривих, які найчастіше використовують в макро- та мікроекономічних дослідженнях. До таких кривих відносяться:

експоненційна 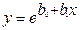; (3.1)

степенева (мультиплікативна) 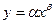; (3.2)

зворотна 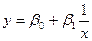. (3.3)

У загальному випадку однофакторну економетричну модель можна подати у вигляді:

У = f(x) + Ɛ,(3.4)

де f(x) — одна з функцій зростання;

Ɛ — випадкова величина.

Як і у випадку з простою лінійною регресією, основне завдання полягає в розрахунку невідомих параметрів кривих зростання і подальшому аналізі обраної моделі. Оцінку невідомих параметрів проводять по-різному: експоненційні функції шляхом логарифмічних перетворень зводять до лінійної регресії, квадратичні функції зводять до багатофакторної регресії, для інших використовують ітеративні методи, метод трьох точок, метод Тейла тощо. Розглянемо функції зростання, які шля­хом перетворень зводяться до лінійної регресії. Для таких функцій збері­гається вся методологія досліджень, яка була детально розглянута у випадку простої лінійної регресії.

Переглядів: 318