• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Cтепенева (мультиплікативна) функція

Степенева функція є однією з найпоширеніших у практиці кривих зростання і описує дуже широкий спектр економічних процесів. Вона має такий вигляд:

у = ax^b. (3.6)

Ми розглядатимемо випадок, коли параметр a ≥ 0, що є типовим для економічних процесів. Якщо значення параметра b — не ціле число, то розглядають лише випадок, коли x ≥ 0. При цьому залежно від знака параметра b степенева функція описуватиме різні економічні процеси: прискорене зростання, уповільнене зростання та спад. Слід зазначити, що якщо b =1, степенева функція перетворюється на лінійну. Ці різні ситу­ації зображені на рисунку 3.1 (а, б,в, г).

Якщо параметр b степеневої функції — ціле число, то залежно від того, парне чи непарне його значення, графік функції має різний вигляд. Якщо b — парне, тобто його можна записати у вигляді: b = 2k, k ε Z (розгляне­мо тільки випадок, коли k > 0), тоді y є [0,+¥), а графік функції симетричний відносно осі ординат (рисунок 3.2, а).

Рисунок 3.1 - Вигляд степеневої функції,

коли b - не ціле число, х ≥ 0

Якщо параметр b — непарне число, тобто його можна подати у вигля­ді: b = 2k - 1, k ε Z₊ (розглянемо тільки випадок, коли k > 0), тоді у є R, а графік функції симетричний відносно початку координат (0,0) (рис. 3.2, б).

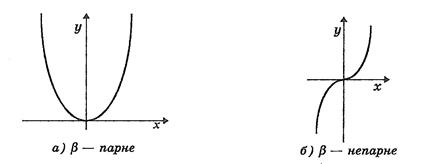
Рисунок 3.2 - Графік степеневої функції,

коли b – ціле число

Звичайно, основне питання полягає в тому, щоб розрахувати невідомі параметри мультиплікативної (степеневої) кривої. Покажемо, що шля­хом логарифмічного перетворення ми можемо легко звести степеневу криву так само, як і експоненційну, до лінійної функції, що дає нам змогу розра­ховувати параметри методом найменших квадратів. Справді, логарифму­ючи праву та ліву частини (3.6), отримаємо:

,

.

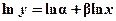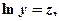
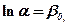
На практиці степеневі функції використовують для опису різних еко­номічних процесів. Найвідомішою з них є виробнича функція Кобба-Дугласа. Крім того, їх застосовують для опису кривих байдужості, а також попиту на товари різних категорій, так звана крива Торнквіста та ін.

Переглядів: 1791