
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Зразок виконання завдання
Завдання: Використовуючи метод сіток, скласти наближений розв’язок 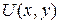
задачі Діріхле для рівняння Лапласа 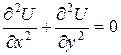 у квадраті АВСD з вершинами
у квадраті АВСD з вершинами 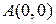 ,
, 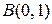 ,
, 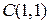 ,
, 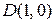 із заданими межовими умовами
із заданими межовими умовами 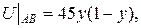
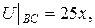
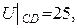
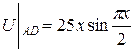 ; крок h=0.2.Відповідь датиз точністю до 0.01.
; крок h=0.2.Відповідь датиз точністю до 0.01.
Розв’язання:
Побудуємо область розв’язку, тобто введемо у квадраті АВСD сітку з кроком h=0.2. Вузли сітки є розрахунковими точками (рис. 11):
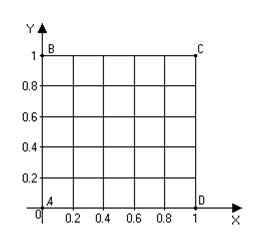
Рис. 11. Сітка області розв’язку
Значення функції 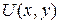 на стороні AB (рис. 2) шукаємо за формулою
на стороні AB (рис. 2) шукаємо за формулою 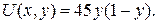 Маємо:
Маємо: 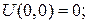
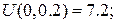
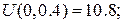
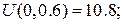
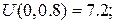
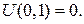
На стороні BС: 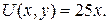 Маємо:
Маємо: 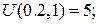
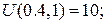
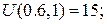
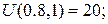
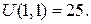
На стороні BС: 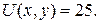 Отже:
Отже: 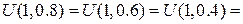
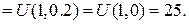
На стороні AD: 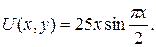 Маємо:
Маємо: 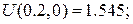
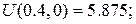
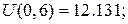
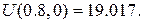
Відмітимо на сітці знайдені межові значення та шукані значення функції 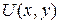 (рис. 12):
(рис. 12):
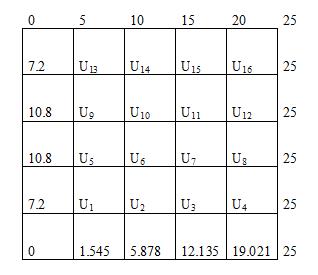
Рис. 12. Розрахункові точки області розв’язку
Для визначення значень функції у внутрішніх точках області розв’язку методом сіток задане рівняння Лапласа у кожній точці замінимо кінцево-різницевим рівнянням за формулою
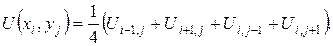
За цією формулою складемо рівняння для кожної внутрішньої точки сітки. В результаті отримаємо систему рівнянь:
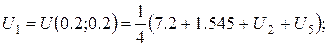
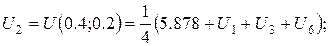
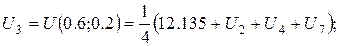
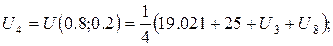
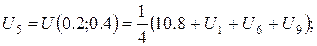
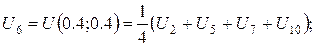
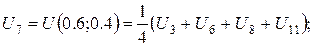
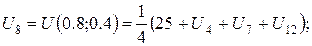
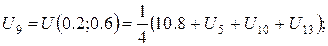
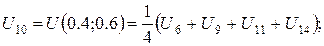
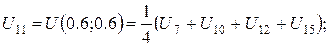
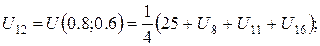
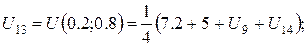
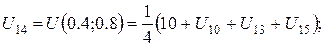
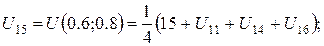
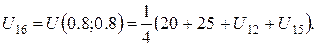
Розв’язок цієї системи будемо шукати ітераційним методом Гауса-Зейделя. Розрахункові співвідношення матимуть вигляд:
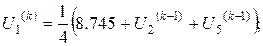
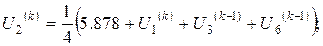
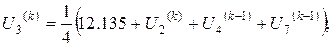
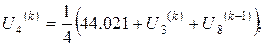
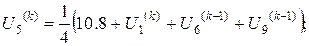
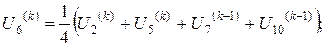
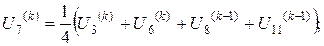
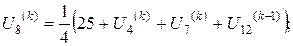
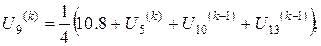
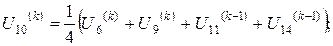
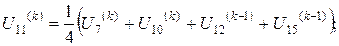
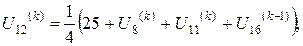
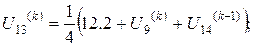
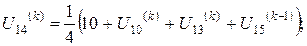

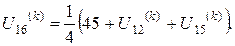
Для проведення обчислень за цими формулами необхідно визначити початкові наближення 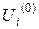 . Припустимо, що функція
. Припустимо, що функція 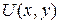 по горизонталях області розв’язку розподілена рівномірно.
по горизонталях області розв’язку розподілена рівномірно.
Розглянемо горизонталь з граничними точками (0, 0.2) та (1, 0.2). Шукані значення функції у внутрішніх точках позначимо через 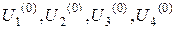 . Оскільки відрізок поділений на 5 частин, то крок зміни функції знаходимо зі співвідношення
. Оскільки відрізок поділений на 5 частин, то крок зміни функції знаходимо зі співвідношення
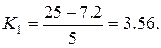
Тоді отримаємо
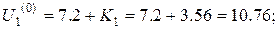
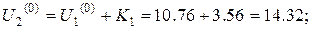
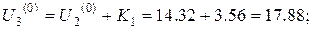
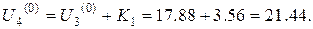
Аналогічні міркування проведемо для знаходження початкових наближень у внутрішніх точках інших горизонталей.
Для другої горизонталі з граничними точками (0, 0.4) та (1, 0.4) маємо
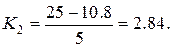
Отже,
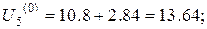
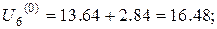
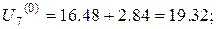
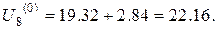
Значення у граничних точках третьої горизонталі такі самі, як й для другої. Тому, 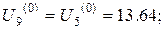
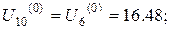
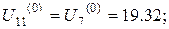
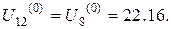
Нарешті, значення у граничних точках четвертої горизонталі такі самі, як й для першої. Отже,
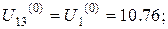
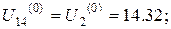
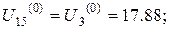
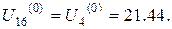
Всі отримані значення розміщуємо у таблиці, яку називають нульовим шаблоном:
| 0.8 | 7.2 | 10.76 | 14.32 | 17.88 | 21.44 | |
| 0.6 | 10.8 | 13.64 | 16.48 | 19.32 | 22.16 | |
| 0.4 | 10.8 | 13.64 | 16.48 | 19.32 | 22.16 | |
| 0.2 | 7.2 | 10.76 | 14.32 | 17.88 | 21.44 | |
| 1.545 | 5.875 | 12.131 | 19.017 | |||
| 0.2 | 0.4 | 0.6 | 0.8 |
Для кожного нового наближеного розв’язку задачі складаємо таблицю, що міститиме лише внутрішні значення, які змінюються в процесі обчислень. Ці таблиці називають шаблонами.
Отримаємо наступну послідовність шаблонів:
Шаблон №1
| Шаблон №2
| ||||||||||||||||||||||||||||||||
Шаблон №3
| Шаблон №4
| ||||||||||||||||||||||||||||||||
Шаблон №5
| Шаблон №6
| ||||||||||||||||||||||||||||||||
Шаблон №7
| Шаблон №8
| ||||||||||||||||||||||||||||||||
Шаблон №9
| Шаблон №10
| ||||||||||||||||||||||||||||||||
Шаблон №11
| Шаблон №12
| ||||||||||||||||||||||||||||||||
Шаблон №13
| Шаблон №14
| ||||||||||||||||||||||||||||||||
Шаблон №15
|
Ітераційний процес зупиняємо, оскільки шаблони №15 та №14 містять послідовні наближення, відхилення між якими стали меншими за 0.01 (задану точність). Результат округлюємо до сотих долей.
Відповідь:
| 0.8 | 7.2 | 8.63 | 11.77 | 15.80 | 20.30 | |
| 0.6 | 10.8 | 10.56 | 12.64 | 16.14 | 20.40 | |
| 0.4 | 10.8 | 10.17 | 12.10 | 15.69 | 20.18 | |
| 0.2 | 7.2 | 7.20 | 9.88 | 14.34 | 19.64 | |
| 1.54 | 5.88 | 12.14 | 19.02 | |||
| 0.2 | 0.4 | 0.6 | 0.8 |
| <== попередня сторінка | | | наступна сторінка ==> |
| Теоретичні відомості | | | Приклад програми |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |