
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Тема: Оптимізація функцій
Завдання: 1) Методом золотого перетину знайти найбільше значення унімодальної функції 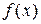 на заданому відрізку
на заданому відрізку 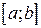 з точністю до 0.01.
з точністю до 0.01.
2) Методом золотого перетину знайти найменше значення унімодальної функції 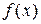 на заданому відрізку
на заданому відрізку 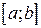 з точністю до 0.01.
з точністю до 0.01.
| Вар. | Функція | 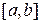
|
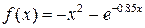
| 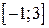
| |
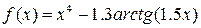
| 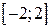
| |
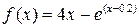
| 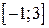
| |
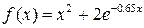
| 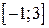
| |
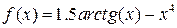
| 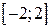
| |
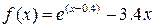
| 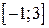
| |
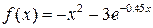
| 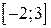
| |
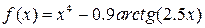
| 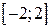
| |
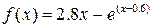
| 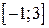
| |
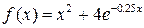
| 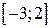
| |
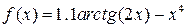
| 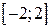
| |
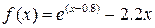
| 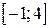
| |
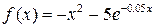
| 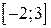
| |
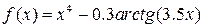
| 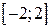
| |
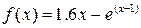
| 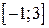
| |
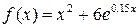
| 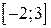
| |
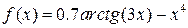
| 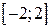
| |
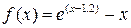
| 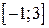
| |
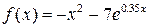
| 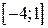
| |
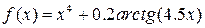
| 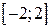
|
Теоретичні відомості.
Під оптимізацією розуміють процес вибору найкращого варіанту з усіх можливих. Більшість задач оптимізації зводиться до пошуку найменшого (найбільшого) значення деякої функції. Методи математичного аналізу зручні для розв’язання цієї задачі, коли функція задається в явному вигляді і при цьому є диференційованою. Коли ж функція задається таблицею значень або має аналітично громіздку формулу, ефективними є числові методи розв'язання.
Існують різні числові методи пошуку для розв’язання задачі оптимізації. Вони засновані на обчисленні функції в окремих точках і виборі серед них найбільшого чи найменшого значення. Процес розв’язання задачі методом пошуку полягає у послідовному звуженні інтервалу зміни параметра функції, який називають інтервалом невизначеності. На початку процесу оптимізації його довжина дорівнює 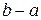 , а по закінченню вона має стати меншою за допустиму похибку
, а по закінченню вона має стати меншою за допустиму похибку 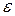 , причому
, причому 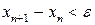 .
.
Метод золотого перетину
Одним з найбільш ефективних числових методів оптимізації функції єметод золотого перетину. Він полягає в побудові послідовності відрізків, що стягуються до точки мінімуму (максимуму) функції. На кожному кроці, за виключенням першого, обчислення значення функції 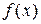 проводяться лише в одній точці, яку називають золотим перетином.
проводяться лише в одній точці, яку називають золотим перетином.
Точка 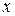 здійснює золотий перетин відрізка
здійснює золотий перетин відрізка 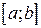 якщо відношення довжини всього відрізка до довжини його більшої частини дорівнює відношенню довжини більшої частини відрізка до довжини його меншої частини (рис. 4):
якщо відношення довжини всього відрізка до довжини його більшої частини дорівнює відношенню довжини більшої частини відрізка до довжини його меншої частини (рис. 4):
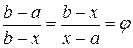 .
.
Число 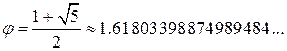 називають золотим числом.
називають золотим числом.
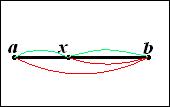
Рис. 4. Золотий перетин відрізка 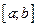 точкою х
точкою х
Зауважимо, що на відрізку 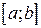 можна визначити дві симетрично розміщені відносно центру відрізка точки (
можна визначити дві симетрично розміщені відносно центру відрізка точки ( 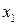 та
та 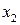 ), що реалізують золотий перетин (рис. 5). Їх знаходимо за формулами:
), що реалізують золотий перетин (рис. 5). Їх знаходимо за формулами:
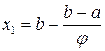 ,
, 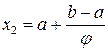 .
.
Якщо 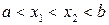 , то очевидно, що точка
, то очевидно, що точка 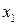 ділить відрізок
ділить відрізок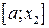 у відношенні золотого перетину. Аналогічно
у відношенні золотого перетину. Аналогічно 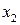 ділить відрізок
ділить відрізок 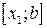 у тій самій пропорції. Ця властивість й використовується для побудови ітераційного процесу.
у тій самій пропорції. Ця властивість й використовується для побудови ітераційного процесу.
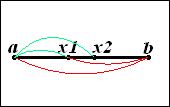
Рис. 5. Точки золотого перетину відрізка 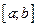
Розглянемо метод золотого перетину на прикладі знаходження мінімуму функції 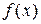 на заданому відрізку. Припустимо, що функція унімодальна, т. б. на даному відрізку вона має лише один мінімум.
на заданому відрізку. Припустимо, що функція унімодальна, т. б. на даному відрізку вона має лише один мінімум.
На першій ітерації в середині відрізка 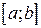 у пропорції золотого перетину обираємо дві внутрішні точки
у пропорції золотого перетину обираємо дві внутрішні точки 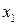 та
та 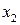 й обчислюємо значення функції у цих точках. Якщо
й обчислюємо значення функції у цих точках. Якщо 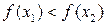 , очевидно, що мінімум функції розташований на одному з відрізків:
, очевидно, що мінімум функції розташований на одному з відрізків: 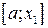 чи
чи 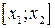 . Тому відрізок
. Тому відрізок 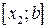 можна відкинути, зменшивши тим самим початковий інтервал невизначеності. Другу ітерацію проводимо на новому відрізку
можна відкинути, зменшивши тим самим початковий інтервал невизначеності. Другу ітерацію проводимо на новому відрізку 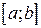 , ввівши позначення:
, ввівши позначення:
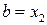 ,
, 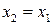 ,
, 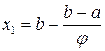 .
.
Якщо ж 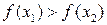 , очевидно, що мінімум функції розташований на одному з відрізків:
, очевидно, що мінімум функції розташований на одному з відрізків: 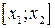 чи
чи 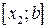 . Отже можна відкинути відрізок
. Отже можна відкинути відрізок 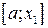 . Другу ітерацію в цьому випадку проводимо на новому відрізку
. Другу ітерацію в цьому випадку проводимо на новому відрізку 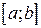 , ввівши позначення:
, ввівши позначення:
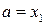 ,
, 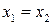 ,
, 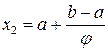 .
.
Знову обчислюємо значення функції 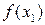 і
і 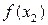 , проводимо порівняння та повторюємо алгоритм звуження інтервалу невизначеності.
, проводимо порівняння та повторюємо алгоритм звуження інтервалу невизначеності.
Процес оптимізації триває до тих пір, поки довжина чергового відрізка 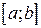 не стане меншою за задану величину
не стане меншою за задану величину 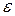 :
:
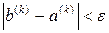 , де
, де 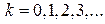
| <== попередня сторінка | | | наступна сторінка ==> |
| Приклад програми | | | Зразок виконання завдання |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |