• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Рћ рациональном выборе РѕСЃРЅРѕРІРЅРѕР№ системы. Р?спользование РїСЂСЏРјРѕР№ Рё обратной симметрии

Рациональной РѕСЃРЅРѕРІРЅРѕР№ системой для заданной статически неопределимой конструкции является такая система, РїСЂРё которой наибольшее число побочных коэффициентов канонических уравнений обращается РІ нуль. Чем больше коэффициентов канонических уравнений равно нулю, тем, очевидно, проще Рё легче решить эти уравнения.

Упрощать решения задачи раскрытия статической неопределимости можно использованием симметричных и обратно симметричных стержневых систем. Отметим, что внутренние силовые факторы в сечении бруса можно также разделить на симметричные и обратно симметричные. К симметричным силовым факторам относятся изгибающие моменты M_y, M_z и нормальные силы N, так как в двух смежных сечениях бруса они симметричны относительно плоскости разреза (рисунок 12.9), а к обратно (косо) симметричным относятся перерезывающие силы Q_y, Q_z и крутящие моменты M_x, поскольку они обратно симметричны относительно плоскости разреза.

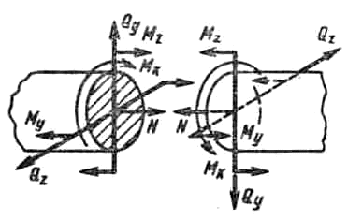
РРёСЃСѓРЅРѕРє 12.9.

Первая группа силовых факторов вызывает симметричные а вторая - обратно симметричные относительно плоскости разреза деформации прилегающих к разрезу частей бруса.

Рассмотрим сначала особенности симметричных стержневых систем. Геометрически симметричная стержневая система СЃ нагрузкой симметричной относительной той же РѕСЃРё (плоскости), называет симметричной.

Вследствие полной симметрии такая система имеет симметричный вид и после деформации. Следовательно, перемещения симметричных сечений симметричны по направлению. Это означает, что в симметричных сечениях симметричной системы одноименные силовые факторы (а в опорных сечениях - опорные реакции) равны по величине и симметричны по направлению.

Если разрезать симметричную систему по оси (плоскости) симметрии, то нетрудно заметить, что обратно симметричные внутренние силовые факторы в этом сечении должны быть равны нули Действительно, обратно симметричные силовые факторы будут вызывать обратно симметричные деформации, которые противоречат характеру деформаций симметричной системы. Таким образом, в сечении по оси симметрии симметричной системы крутящие моменты M_x и перерезывающие силы Q_y, Q_z всегда равны нулю.

Покажем справедливость этих выводов РЅР° примере плоской симметричной рамы (СЂРёСЃСѓРЅРѕРє 12.10). Эта рама представляет СЃРѕР±РѕР№ плоский замкнутый контур Рё является трижды статически неопределимой системой. Выберем РѕСЃРЅРѕРІРЅСѓСЋ систему разрезом РїРѕ РѕСЃРё симметрии. Допустим, что РІСЃРµ внутренние силовые факторы - изгибающие моменты X₁, нормальные силы X₂ Рё перерезывающие силы X₃ - отличны РѕС‚ нуля.

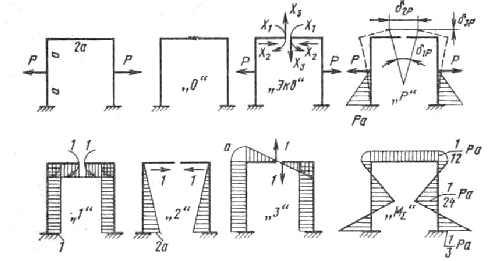
РРёСЃСѓРЅРѕРє 12.10.

Раскрывая статическую неопределимость задачи методом СЃРёР», запишем систему канонических уравнений

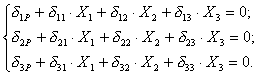
Для вычисления ее коэффициентов построим эпюры изгибающих моментов от заданной и единичных нагрузок (см. рисунок 12.10).

Эпюры от заданных нагрузок, изгибающих моментов и нормальных сил симметричны, а от перерезывающих сил - обратно симметричны. Произведение симметричной эпюры на обратно симметричную равно нулю, поэтому коэффициенты канонических уравнений

.

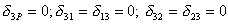В результате система канонических уравнений принимает вид

Коэффициент Оґ₃₃ отличен РѕС‚ нуля Рё поэтому перерезывающая сила X₃ равна нулю.

Р?так, РІ сечении РїРѕ РѕСЃРё симметрии симметричной стержневой системы обратно симметричные силовые факторы равны нулю.

Вычисляя остальные коэффициенты канонических уравнений, получаем

.

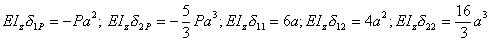Решая систему канонических уравнений, находим

.

Суммарная СЌРїСЋСЂР° изгибающих моментов симметрична относительно РѕСЃРё симметрии рамы, так как ее ординаты представляй СЃРѕР±РѕР№ СЃСѓРјРјС‹ ординат симметричных СЌРїСЋСЂ В«PВ», В«1В» Рё В«2В» (ординаты РґРІСѓС… последних увеличиваются соответственно РІ X₁ Рё X₂ раз). Таким образом, подтверждено Рё второе свойство симметричных систем: силовые факторы РІ симметричных сечениях симметричной стержневой системы равны РїРѕ величине Рё симметричны РїРѕ направлению.

Р?так, РѕСЃРЅРѕРІРЅСѓСЋ систему РІ симметричных конструкциях надо выбирать путем удаления лишних связей РЅР° РѕСЃРё симметрии Рё следить Р·Р° тем, чтобы Рё эквивалентная система была симметричной (только РїСЂРё этом условии реализуются свойства симметричных систем). Если РІ конструкции имеется стержень, направленный вдоль РѕСЃРё симметрии, то РѕСЃРЅРѕРІРЅСѓСЋ систему надо выбирать путем удаления лишних связей РІ симметричных сечениях.

Переглядів: 736