• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Пример 12.2

Построить эпюру изгибающих моментов для рамы, представленной на рисунок 12.8.

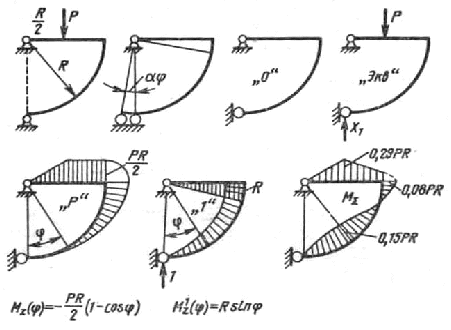
РРёСЃСѓРЅРѕРє 12.8.

Рама РѕРґРёРЅ раз статически неопределима. Выберем РѕСЃРЅРѕРІРЅСѓСЋ систему, удаляя РѕРґРЅСѓ СЃРІСЏР·СЊ РІ нижнем (или верхнем) шарнире. Однако РІ рассматриваемой раме горизонтальные Рё вертикальные опорные СЃРІСЏР·Рё неравноценны. Если удалить горизонтальную СЃРІСЏР·СЊ, то РїСЂРё любой нагрузке реакция R_y оставшейся вертикальной РІСЏР·Рё должна быть бесконечно большой, так как линия ее действия РїСЂРѕС…РѕРґРёС‚ через центр верхнего шарнира, Р° момент внешней нагрузки относительно этого шарнира РЅРµ равен нулю. Чтобы воспринять даже самую малую нагрузку, эта рама должна сначала повернуться как жесткое целое (без деформации) РЅР° бесконечно малый СѓРіРѕР» dП†. РўРѕРіРґР° плечо реакции R_y станет отличным РѕС‚ нуля, Р° сама реакция будет конечной, РЅРѕ значительной РїРѕ величине.

Такая система является мгновенно геометрически изменяемой. Ее в качестве основной системы выбирать нельзя.

Положение сразу же изменяется, если удалить не горизонтальную, а вертикальную опорную связь. В такой основной системе при любой нагрузке опорные реакции и внутренние силовые факторы будут конечными и определенными. Эквивалентная система, соответствующая этой основной системе, представлена на рисунок 12.8. Там же приведены эпюры изгибающих моментов от заданной и единичных нагрузок.

Вычисляя коэффициенты канонического уравнения Оґ_1P+Оґ₁₁X₁=0 интегрированием РЅР° криволинейных участках Рё перемножением СЌРїСЋСЂ РЅР° прямолинейных, получаем

;

.

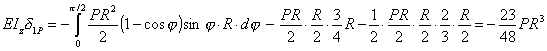Отсюда

.

Суммарный изгибающий момент на криволинейном участке изменяется по закону

.

Приравнивая нулю производную от M_Σ(φ):

,

получаем

.

Следовательно, при φ=40° функция M_Σ(φ) имеет экстремум, причем M_Σ(45°)=0.15PR. Суммарная эпюра приведе на на рисунок 12.8.

Определение перемещений в статически неопределимых системах

После раскрытия статической неопределимости и построения суммарных эпюр силовых факторов можно приступить к определению перемещений сечений рассматриваемой стержневой системы. Естественно это делать методом Мора, перемножая, где возможно, по правилу Верещагина суммарные эпюры внутренних силовых факторов на соответствующие эпюры от единичных нагрузок, приложенных в сечениях, перемещения которых определяются.

Однако построение эпюр от единичных нагрузок при приложении их непосредственно к заданной системе требует вторичного раскрытия ее статической неопределимости. Такой достаточно трудоемкой операции можно избежать, если определять перемещения не в заданной, а в эквивалентной системе. Причем не обязательно пользоваться первоначальной эквивалентной системой, выбранной для раскрытия статической неопределимости, так как перемещения одного и того же сечения во всех системах, эквивалентных данной, одинаковы.

Если сечение заданной системы РІ рассматриваемом направлении РЅРµ перемещается, то произведение суммарной СЌРїСЋСЂС‹ РЅР° единичную должно быть равно нулю. РќР° этом свойстве основана проверка правильности вычисления неизвестных X₁, X₂, X₃,...X_n РїСЂРё раскрытии статической неопределимости Рё построения суммарных СЌРїСЋСЂ.

Абсолютные или относительные перемещения сечений РІ направлении усилий X₁, X₂, X₃,...X_n отсутствуют, поэтому произведение каждой РёР· единичных СЌРїСЋСЂ РЅР° суммарную должно быть обязательно равно нулю. Пользуясь этим правилом, нетрудно проверить, что суммарная СЌРїСЋСЂР° изгибающих моментов РІ примере 12.1 построена правильно, так как произведение этой СЌРїСЋСЂС‹ РЅР° первую единичную (СЃРј. СЂРёСЃСѓРЅРѕРє 12.7)

.

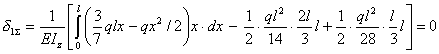Ордината суммарной эпюры, под центром тяжести второй единичной эпюры, как видно из рисунка 12.7, равна нулю. Следовательно, произведение и этих двух линейных эпюр также равно нулю.

Читайте також:

1. Пример 10.2
2. Пример 10.3
3. Пример 12.1
4. Пример 12.3
5. Пример 12.5
6. Пример 12.6
7. Пример 13.1
8. Пример 13.2
9. Пример 15.2
10. Пример 15.3
11. Пример 3.1

Переглядів: 792