
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Расчет РЅР° устойчивость СЃ помощью коэффициента снижения РѕСЃРЅРѕРІРЅРѕРіРѕ допускаемого напряжения
Вместо РґРІСѓС… формул (Рйлера Рё РЇСЃРёРЅСЃРєРѕРіРѕ), каждая РёР· которых РїСЂРёРіРѕРґРЅР° для определенного диапазона гибкостей, удобнее иметь РѕРґРЅСѓ формулу, которой можно пользоваться РїСЂРё любой гибкости стержня.
Рта практическая формула, широко применяющаяся РїСЂРё расчете строительных конструкций, имеет следующий РІРёРґ:
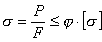 , ,
| (13.19) |
где [σ] - основное допускаемое напряжение на сжатие; φ - коэффициент снижения основного допускаемого напряжения (или коэффициент продольного изгиба); F - площадь поперечного сечения стержня.
Величина φ зависит от материала и гибкости стержня. Его значения приведены в таблице 13.1.
Величина φ[σ] может рассматриваться как допускаемое напряжение при расчете на устойчивость, т. е.
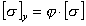 . .
| (13.20) |
Таблица 13.1.
| Гибкость, λ | φ для | ||||
| сталей Ст 1,2,З,4 | стали Ст5 | стали повышенного качества ?σпц>320 МПа | чугуна | дерева | |
| 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 0.99 | 0.98 | 0.97 | 0.97 | 0.99 | |
| 0.96 | 0.95 | 0.95 | 0.91 | 0.97 | |
| 0.94 | 0.92 | 0.91 | 0.81 | 0.93 | |
| 0.92 | 0.89 | 0.87 | 0.69 | 0.87 | |
| 0.89 | 0.86 | 0.83 | 0.57 | 0.80 | |
| 0.86 | 0.82 | 0.79 | 0.44 | 0.71 | |
| 0.81 | 0.76 | 0.72 | 0.34 | 0.60 | |
| 0.75 | 0.70 | 0.65 | 0.26 | 0.48 | |
| 0.69 | 0.62 | 0.55 | 0.20 | 0.38 | |
| 0.60 | 0.51 | 0.43 | 0.16 | 0.31 | |
| 0.52 | 0.43 | 0.35 | - | 0.25 | |
| 0.45 | 0.37 | 0.30 | - | 0.22 | |
| 0.40 | 0.33 | 0.26 | - | 0.18 | |
| 0.36 | 0.29 | 0.23 | - | 0.16 | |
| 0.32 | 0.26 | 0.21 | - | 0.14 | |
| 0.29 | 0.24 | 0.19 | - | 0.12 | |
| 0.26 | 0.21 | 0.17 | - | 0.11 | |
| 0.23 | 0.19 | 0.15 | - | 0.10 | |
| 0.21 | 0.17 | 0.14 | - | 0.09 | |
| 0.19 | 0.16 | 0.13 | - | 0.08 |
Для подбора сечения формулу (13.19) приводят к следующему виду:
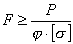 .
.
При этом значением φ приходится задаваться, так как гибкость λ неизвестна, ибо неизвестна площадь сечения F, а гибкость зависит от нее. В качестве первого приближения рекомендуется принимать φ1=0,5. Затем определяют величины F, Imin, imin, λ и по таблице 13.1 находят соответствующее значение φ1.
Если получается большая разница между значениями φ1 и φ2, то следует повторить расчет, задавшись новым значением φ2:
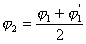
и т. д., пока разница между последовательными значениями не будет превышать 4-6%.
Для стержней, сечения которых имеют значительные ослабления (например, от отверстий), кроме расчета на устойчивость должен производиться и обычный расчет на прочность по формуле
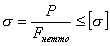 ,
,
где F - рабочая (нетто) площадь сечения стержня.
При расчете же на устойчивость берется полная площадь сечения Fбрутто.
Р’ некоторых случаях (например, РїСЂРё расчете элементов машиностроительных конструкций) значения коэффициентов запаса устойчивости, предусмотренные РїСЂРё составлении таблиц коэффициентов П† (ny≈1.8), недостаточны. Р’ этих случаях расчет следует вести, РёСЃС…РѕРґСЏ непосредственно РёР· требуемого коэффициента ny Рё пользуясь формулой Рйлера или РЇСЃРёРЅСЃРєРѕРіРѕ. Так же следует поступать РїСЂРё расчете РЅР° устойчивость стержней РёР· материалов, которые РЅРµ отражены РІ таблице коэффициентов П†.
Рациональные формы сечений сжатых стержней
РџСЂРё заданных нагрузке, длине стержня, допускаемом напряжении форма Рё размеры поперечного сечения сжатого стержня характеризуются радиусом инерции. Радиус инерции величина размерная. Для сравнения различных сечений между СЃРѕР±РѕР№ более СѓРґРѕР±РЅРѕР№ является безразмерная величина
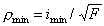 , ,
| (13.21) |
которую называют удельным радиусом инерции.
В таблице 13.2 приведены значения ρmin для некоторых наиболее распространенных сечений:
Таблица 13.2.
| Тип сечения | ρmin |
| Прямоугольник при h/b=2 | 0.204 |
| Квадрат | 0.289 |
| РљСЂСѓРі | 0.36 |
| Двутавр | 0.27-0.41 |
| Швеллер | 0.38-0.45 |
| Уголки равнобокие | 0.4-0.6 |
| Кольцо при α=0.7-0.9 | 0.86-1.53 |
Как видно из таблицы 13.2, наименее выгодными являются прямоугольные сплошные сечения, у которых моменты инерции относительно главных осей не равны между собой и, следовательно, не соблюдается принцип равной устойчивости стержня в обеих главных плоскостях инерции.
Наиболее выгодными являются кольцевые, а также коробчатые тонкостенные сечения. Подсчеты показывают, что замена сжатых сечений в виде уголков и двутавров трубчатыми стержнями дает экономию в материале до 20-40%.
Читайте також:
- Расчет заклепочного соединения
- Расчеты РЅР° прочность Рё жесткость РїСЂРё кручении
- Расчеты РЅР° прочность РїСЂРё поперечном РёР·РіРёР±Рµ
| <== попередня сторінка | | | наступна сторінка ==> |
| Пример 13.1 | | | Пример 13.2 |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |