
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Рівняння Нав'є-Стокса .
Виділимо в потоці рідини, що рухається по каналу, елементарний паралелепіпед з ребрами dx,dy,dz (рис.3.2.1). На цей елемент діють три сили: сила тяжіння, сила тиску і сила тертя.

Рис. 3.2.1. До виведення диференційного рівняння руху в'язкої рідини ,що не стискується
. Сила тяжіння може бути визначена з виразу :
G=g×r×dx×dy×dz
де р- густина рідини;
g- прискорення вільного падіння.
V=dx×dy×dz ,
де V-об¢єм паралелепіпеда .
Силу тиску можна знайти з наступних міркувань. Гідростатичний тиск в даному випадку змінюється вздовж вертикальної вісі. Нехай на верхній грані значення тиску р, тоді на верхню грань діє сила:
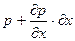 P=p×dy×dz(Рис.2.1.2..б). Тиск біля нижньої грані елемента рівний :
P=p×dy×dz(Рис.2.1.2..б). Тиск біля нижньої грані елемента рівний :
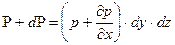 |
тому сила тиску рівна:
Результуюча цих сил і буде силою тиску, що діє на елемент:


(3.2.1)
Силу тертя виразимо виходячи з припущень про плоско-паралельний рух потоку. В цьому випадку локальні швидкості руху частинки в потоці WX(рис. 3.2.1 б) змінюються лише в напрямку вісі у, а тертя виникає лише на бічних гранях AB і CD. Біля грані AB швидкість руху рідини менше, ніж швидкість руху виділеного елементу, тому сила тертя напрямлена проти руху. Якщо силу тертя, віднесену до одиниці поверхні, позначити через s¢, то сила тертя, що діє на грань AB, буде S=s¢×dx×dz .
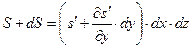 (3.2.2)
(3.2.2)
Біля грані CD швидкість руху частинок більша , за швидкість руху елемента, і силу тертя, напрям котрої співпадає з напрямом руху елемента, можна виразити як
Результуюча зазначених сил і є сила тертя, що діє на елемент потоку рідини:
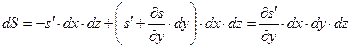 (3.2.3)
(3.2.3)
| |
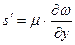
Тому силу тертя можна виразити як :
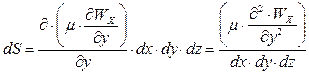 (3.2.4)
(3.2.4)
На основі другого закону механіки (рівнодіюча сила дорівнює масі, помноженій на прискорення) для даного випадку запишемо:
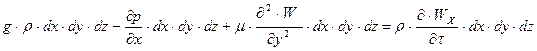 |
 (3.2.5)
(3.2.5)
це диференційне рівняння для рівномірного сталого руху незріджуючої в'язкої рідини. ,що не стискується .
Для випадку трьохмірного несталого руху в'язкої рідини ( r=const ),що не стискується отримують більш складні рівняння, але структура їх зберігається:

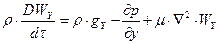 (3.2.6)
(3.2.6)

Рівняння (2.1.6) руху в’язкої рідини , що не стискується називають рівняннями Нав"є-Стокса. Де похідні DWX/dt , DWY/dt , DWZ/dt в лівій частині рівняння (3.2.6) являють собою повні похідні швидкості по часу:

 (3.2.7)
(3.2.7)
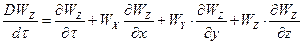
Перші члени доданків правих частин рівнянь (3.2.7) визначають локальні зміни складових швидкості у часі. Три останні доданки правих частин рівнянь враховують переміщення елементу рідини з однієї точки простору в іншу.
Величини gХ, gУ, gZ - складові рівняння вільного падіння в напрямку окремих вісів координат.
Символом V2 (набла) позначений оператор Лапласа, що є сума других похідних:
 (3.2.8)
(3.2.8)
| <== попередня сторінка | | | наступна сторінка ==> |
| Кінетика фільтрування | | | Отримання чисел подібності з диференційного рівняння для рівномірного сталого руху рідини ,що не стискується |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |