• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Отримання чисел подібності з диференційного рівняння для рівномірного сталого руху рідини ,що не стискується

В зв’язку зі складністю аналітичного розв’язку вище приведених систем рівнянь, використаємо рівняння подібності руху рідини .

Всі члени рівняння (3.2.5) мають розмірність сили, що віднесена до об’єму. Для приведення рівняння до безрозмірного виду розділимо всі його члени на 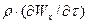,в результаті отримаємо:

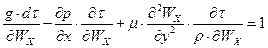(3.3.1)

Кожен доданок лівої частини рівняння (3.3.1) безрозмірний. З них можна отримати числа подібності. Для цього викреслимо символи диференціювання і символи, що характеризують напрям (заміна х і у не орієнтованим в певному напрямку лінійним розміром ) .

1). З першого доданку отримаємо число Фруда,яке характеризує відношення сил тяжіння до інерційних сил:

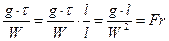(3.3.2)

2). З другого доданку отримаємо число Ейлера, що характеризує відношення сил тиску в потоці до інерційних сил:

(3.3.3)

3). Третій доданок дає величину, зворотну числу Рейнольдса :

(3.3.4)

Числа Re, Eu, Fr отримані з рівнянь Нав’є-Стокса (3.2.6). Крім цього з цих рівнянь додатково можна отримати число гомохромності, що враховує несталий характер руху в подібних потоках:

(3.3.5)

В рівняння подібності, що описує рух потоку фільтруємої рідини, не вводиться число Фруда, оскільки при фільтруванні сили тяжіння настільки малі в зрівнянні з силами тиску та тертя, що ними можна знехтувати. Для устаткованого режиму в рівняння подібності не вводиться критерій гомохронності. Крім того, в рівняння подібності вводять параметричний критерій l/d_ек ,який характеризує геометричні особливості системи, яка розглядається.

Рівняння подібності, що описує рух потоку фільтруючої рідини, наводять в наступному вигляді:

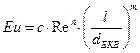(3.3.6)

Читайте також:

1. N – чисельність популяції
2. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
3. Агрегативна стійкість, коагуляція суспензій. Методи отримання.
4. Аеровані промивальні рідини
5. Аксіома неперервності дійсних чисел
6. Алгоритми переведення чисел з однієї позиційної системи числення в іншу
7. Аналіз чисельності, складу і руху персоналу
8. Аналогія - спосіб отримання знань про предмети та явища на основі їхньої подібності з іншими.
9. Асимптотичний підхід до порівняння оцінок
10. Аудиторські докази: поняття та процедури отримання
11. Бюджетний контроль - це порівняння показників бюджету зі звітом за від­повідний період часу.
12. В обох випадках основним розрахунковим рівнянням є рівняння теплопередачі і теплового балансу

Переглядів: 559