Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

ОПЕРАЦIЙНИМИ ПIДСИЛЮВАЧАМИ

ПЕРЕДАТНI ФУНКЦІЇ СХЕМ З

Узагальнений метод вузлових потенцiалiв можна поширити на схеми з операцiйними пiдсилювачами (ОП). Iдеальний ОП є джерелом напруги, яке керується напругою (ДНКН), з коефiцiєнтом пiдсилення , який прямує до нескiнченностi. Реальний ОП - це багатокаскадний транзисторний пiдсилювач в iнтегральному виконаннi, у якого i практично виконуються вимоги: вхiдний опiр 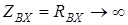, вихiдний опiр 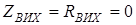. Умовне позначення та еквiвалентна схема ОП зображені на рис.14.1а,б. На схемi iнвертувальний вхiд ОП позначено символом p, прямий вхiд - q, вихiд - r.

Оскiльки ОП має 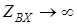, вхiднi струми 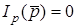; 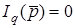. Врахуємо в схемi (рис.14.1б) скінчене значення вихiдного опору 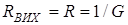та перейдемо до джерела струму (рис.14.1в). Врахуємо, що змiна напряму джерела обумовлена змiною знака.

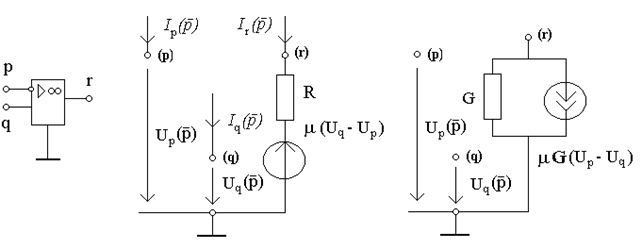
а) б) в)

Рисунок 14.1

Складемо для схеми (рис.14.1в) матрицю провiдностей операцiйного пiдсилювача

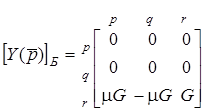. (14.1)

У вiдповiдностi з правилом, отриманим у попереднiй лекцiї, додамо матрицю (14.1) до матрицi схеми та пiдсумуємо провiдностi у комiрках зі збіжними номерами (p, r, q).

. (14.2)

Розкриємо визначник i алгебраїчнi доповнення матрицi (14.2) за елементами r-го рядка у вiдповiдностi до правила (13.15).

;

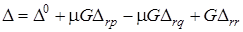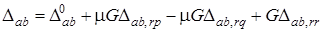; (14.3)

Пiдставимо (14.3) до (10.5)

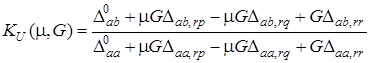Вiдповiдно до (13.7)

де p, q - номери стовпцiв, що пiдсумовуються, r - номер рядка.

Тоді

. (14.4)

Врахуємо, що для ОП , , 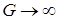i знайдемо коефiцiєнт передачi, послiдовно використовуючи граничнi переходи

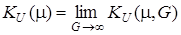; (14.5)

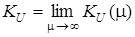. (14.6)

Згiдно з формулою (14.5), одержимо

. (14.7)

Згiдно з формулою (14.6) матимемо

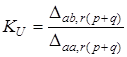. (14.8)

Для схеми з ОП у триполюсному увiмкненнi (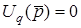) коефiцiєнт передачi розраховується за формулою

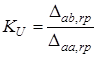. (14.9)

Для каскадного з’єднання n ОП у триполюсному увiмкненнi (рис.14.2) коефiцiєнт передачi розраховується за формулою

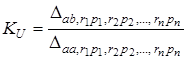. (14.10)

Рисунок 14.2

Для каскадного з’єднання n ОП у диференцiйному увiмкненнi (рис.14.3) матимемо

. (14.11)

Рисунок 14.3

Приклад 1. Визначити операторний коефiцiєнт передачi для схеми (рис.14.4).

1. Пронумеруємо вузли i встановимо вiдповiднiсть мiж цифровими та функцioнальними позначеннями iндексiв: a = 1; b = 4, r = 4; p = 3; q = 5.

2. Для схеми без ОП маємо . З урахуванням ОП згiдно з (14.9) отримуємо .

Рисунок 14.4

3. Складемо матрицю схеми з ОП

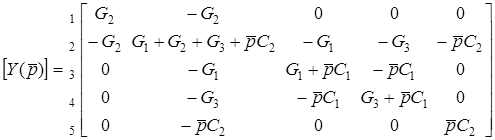4. Перевiримо на рiвнiсть нулю суми елементiв всiх рядкiв та стовпцiв.

5. Викреслимо п'ятий рядок i п'ятий стовпець, оскiльки згiдно з правилом 4 (лекцiя 13) заземленню вузла вiдповiдає викреслення рядка i стовпця.

6. Розрахуємо алгебраїчнi доповнення за правилом (13.9)

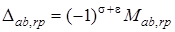Для визначення чисельника викреслюємо 4-й i 3-й стовпцi та 1-й i 4-й рядки. Сума iндексiв складає s = 1+4+4+3 = 12, кiлькiсть iнверсiй e = 1. Отже, чисельник матиме знак "мiнус". Запишемо алгебраїчне доповнення чисельника з урахуванням знака

Для визначення знаменника викреслюємо 1-й i 3-й стовпцi та 1-й i 4-й рядки. Сума iндексiв дорiвнює s = 1+1+4+3 = 9, iнверсiй нема. Отже, матимемо:

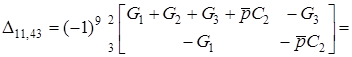
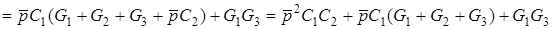Пiдставивши цi значення до формули , отримаємо:

. (14.12)

Тобто є ДРФ вигляду (11.6) з коефiцiєнтами ; ; ; 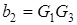. Цей вираз вiдповiдає ланцi другого порядку типу ФНЧ.

Розглянутий приклад дозволяє зробити такі висновки:

1. Якщо вiдомi параметри кола R i C, можна пiдставити їх значення в (14.12) i розрахувати , тобто розв'язати задачу аналiзу.

2. Якщо вiдомий вигляд функцiї та числовi значення коефiцiєнтiв 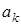, , 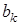можна розв'язати обернену задачу (задачу синтезу) i розрахувати параметри кола R, C.

3. Перехiд до частотних характеристик здiйснюється за загальними правилами

;

- АЧХ ;

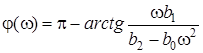- ФЧХ .

Аналiз АЧХ та ФЧХ пiдтверджує, що передатна функцiя (14.12) вiдповiдає схемi ФНЧ.

Приклад 2. Визначити операторний коефiцiєнт передачi для схеми (рис.14.5).

1.Пронумеруємо вузли i встановимо вiдповiднiсть мiж цифровими та функцioнальними позначеннями iндексiв: a = 1; b = 6, r = 4; p = 2; q = 3; r = 6; p = 5; q = 7.

2. Згiдно з даною нумерацiєю запишемо формулу для коефiцiєнта передачi для каскадного з’єднання першого ОП у диференцiйному увiмкненнi та другого ОП у трихполюсному увiмкненнi

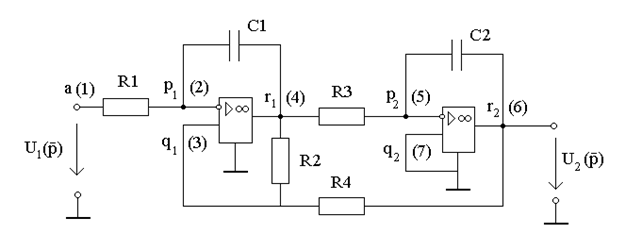
Рисунок 14.5

3. Складемо матрицю схеми з ОП

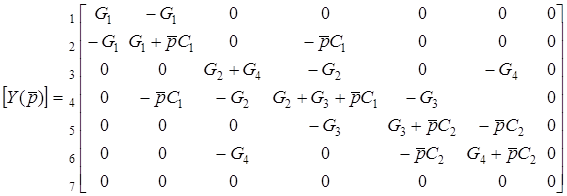4. Перевiримо на рiвнiсть нулю суми елементiв всiх рядкiв та стовпцiв.

5. Викреслимо сьомий рядок i сьомий стовпець, оскiльки згiдно з правилом 4 (лекцiя 13) заземленню вузла вiдповiдає викреслення рядка i стовпця.

6. Викреслимо рядки 1,4,6 та стовпець 5, а стовпцi 2 та 3 об'єднаємо за правилом 7 (тобто перенесемо елементи стовпця 2 до стовпця 3). Тодi скорочена матриця матиме вигляд

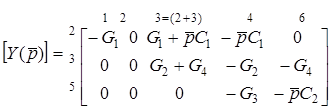7. Розрахуємо алгебраїчнi доповнення за правилом 6 (13.9)

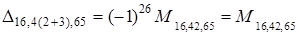Для визначення чисельника викреслюємо другий стовпець. За правилом 7 знак сумарного алгебраїчного доповнення визначається першим iндексом у дужках (тобто 2). Тодi сума iндексiв складатиме s = 1+6+4+2+6+5 = 24, кiлькiсть iнверсiй - двi: iндекси стовпцiв треба послiдовно переставити 625 ® 265 ® 256. Отже, чисельник матиме знак "плюс". Запишемо алгебраїчне доповнення чисельника з урахуванням знака

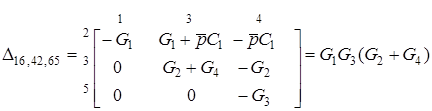8. Аналогiчно отримуємо вираз для знаменника

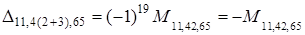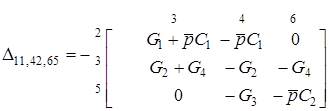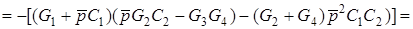
Отже, коефiцiєнт передачi розраховується за формулою

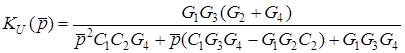Цей коефiцiєнт також вiдповiдає ланцi другого порядку типу ФНЧ.

<== попередня сторінка	\|	наступна сторінка ==>
БАГАТОПОЛЮСНИМИ ЕЛЕМЕНТАМИ	\|	КОЛА З РОЗПОДIЛЕНИМИ ПАРАМЕТРАМИ. ДОВГI ЛIНIЇ

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.009 сек.