• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

КОЛА З РОЗПОДIЛЕНИМИ ПАРАМЕТРАМИ. ДОВГI ЛIНIЇ

15.1 Основнi поняття та означення

До цього часу в курсi ОТК розглядалися сигнали 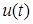, якi змiнюються тiльки у часi. Але iснують також сигнали, якi змiнюються як у часi, так i у просторi. Такий сигнал зветься хвилею.

Кола з розподiленими параметрами характеризуються iснуванням в них хвильових процесiв, при яких напруга 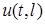i струм 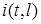змiнюються не тiльки за часом , але i у просторi. Характер змiнювання цих величин у просторi може бути близьким у деякому вiдношеннi до закону їх змiнювання у часi. Якщо, наприклад, на входi кола дiє синусоїдна е.р.с., то в будь-якiй точцi кола з координатою 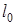значення напруги (струму) повторюється через перiод T: 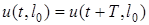. При цьому в будь-який фiксований момент часу значення напруги (струму) може повторюватися через деякий просторовий iнтервал 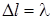: (рис.15.1). Величина зветься довжиною хвилi.

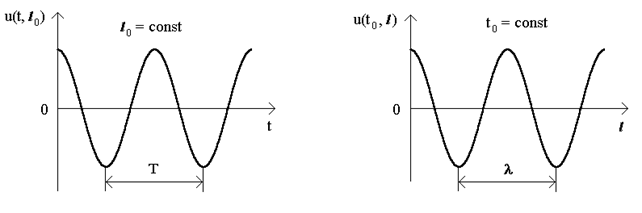
Рисунок 15.1

У загальному випадку коло характеризується трьома лiнiйними розмiрами x, y, z. Якщо x << l; ; 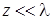, то коло є системою з зосередженими параметрами. При цьому, по-перше, час запiзнення електромагнiтних коливань у колi 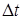значно менший за перiод коливань генератора, ; а по-друге, миттєве значення напруги (струму) однакове у будь-якiй точцi кола.

Iз зменшенням довжини хвилi (iнакше, iз збiльшенням частоти f) вказанi умови не виконуються, i тодi коло буде системою з розподiленими параметрами (хвилеводною системою).

Розглянемо окремий випадок хвилеводних систем, у яких ; ; 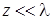. Такi системи звуться колами з лiнiйно-розподiленими параметрами або електричними довгими лiнiями. Струм i напруга в лiнiї є функцiями лiнiйної координати x (або l).

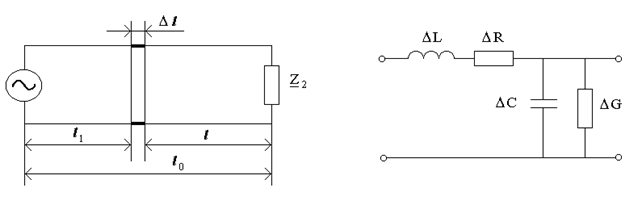
Довгi лiнiї є основним елементом будь-якої системи електрозв'язку. В технiцi радiозв'язку прикладом лiнiй є так званi фiдери. Наприклад, двопровiдна лiнiя зв'язку (рис.15.2а) i коаксiальна лiнiя (рис.15.2б). Лiнiї використовуються для передавання електромагнiтної енергiї вiд передавача до антени, вiд антени до приймача та iн. Довгi лiнiї (ДЛ) застосовуються також як елементи радiоапаратури в дiапазонi НВЧ (фазообертачi, лiнiї затримки тощо).

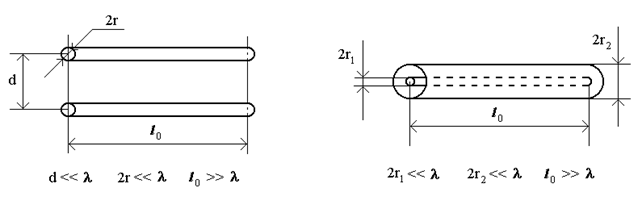
а) б)

Рисунок 15.2

15.2 Первиннi параметри лiнiї

Безпосередньо описати систему з розподіленими параметрами за допомогою рiвнянь Кiрхгофа неможливо, тому що миттєвi значення напруги 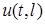i струму 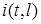залежать вiд розмiру кола та часу розповсюдження електромагнiтних хвиль. Разом з тим, будь-яку дiлянку лiнiї довжиною 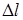можна подати у виглядi еквiвалентної схеми, яка складається з зосереджених нескiнченно малих елементiв 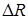, , , , 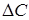для яких закони теорiї кiл слушнi повною мiрою (рис.15.3а,б).

а) б)

Рисунок 15.3

Для кількісної оцiнки величин 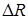, , , 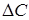використовуються так званi первиннi параметри лiнiї, якi розраховуються на одиницю довжини:

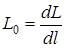- первинна iндуктивнiсть, Гн/м (мкГн/м);

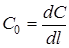- первинна ємнiсть, Ф/м (пФ/м);

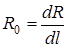- первинний опiр втрат, Ом/м;

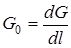- первинна провiднiсть, См/м.

Якщо вiдомi первиннi параметри, тодi 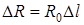; ; 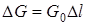; 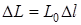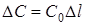. Первиннi параметри залежать вiд частоти i конструкцiї лiнiї. Формули для розрахунку первинних параметрiв одержуються в теорiї поля та наводяться у довiдниках.

Якщо первиннi параметри не змiнюються вздовж лiнiї, то лiнiя зветься однорiдною. При синусоїдній дiї використовують поняття первинного комплексного опору i первинної комплексної провiдностi

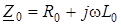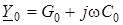; . (15.1)

15.3 Диференцiйнi рiвняння довгої лiнiї

Отже, щоб скористатись законами Кiрхгофа, розглянемо вiдрiзок лiнiї нескiнченно малої довжини з зосередженими параметрами (рис.15.4). Згiдно з другим законом Кiрхгофа

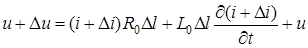. (15.2)

Рисунок 15.4

У (15.2) використовуються частиннi похiднi, оскiльки напруга u та струм i залежать не тiльки вiд часу, але i вiд координати l.

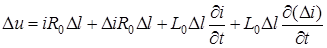. (15.3)

Виключивши з формули (15.3) доданки другого порядку малостi та подiливши обидвi частини на 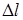, отримуємо

.

Переходячи вiд 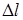до 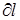, матимемо

. (15.4)

Аналогiчно отримуємо рiвняння для струму, використавши перший закон Кiрхгофа: ;

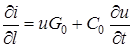. (15.5)

Координата l у даних формулах вiдраховувалася вiд навантаження. Якщо координату вiдраховувати вiд генератора, треба зробити замiну 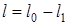, де 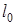- довжина лiнiї. Тодi з (15.4) та (15.3) отримуємо

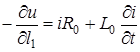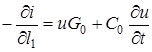; . (15.6)

Диференцiйнi рiвняння (15.6), якi визначають миттєвi значення струму та напруги в лiнiї, звуться телеграфними рiвняннями. Назва обумовлена iсторично першим застосуванням довгих лiнiй для передачi телеграфних сигналiв.

15.4 Розв'язання диференцiйних рiвнянь при усталеній синусоїдній дії

Аналiтичний розв'язок телеграфних рiвнянь для довiльної дії відсутній. Але положення суттєво спрощується у разi усталеної синусоїдної дії. Тодi можна застосувати символiчний метод (метод комплексних амплiтуд):

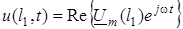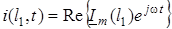; . (15.7)

Оскiльки в усталеному режимi закон змiнювання струму та напруги у часi вiдомий, телеграфнi рiвняння переходять з рiвнянь у частинних похiдних у звичайнi диференцiйнi рiвняння

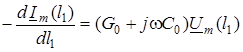; . (15.8)

Для розв'язування рiвнянь (15.8), треба роздiлити в них змiннi 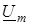та 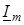. Для цього продиференціюємо рiвняння по :

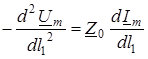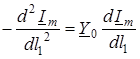; . (15.9)

Пiдставивши в (15.9) значення перших похiдних з (15.8), отримуємо так званi хвильовi рiвняння

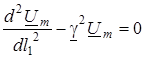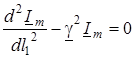; , (15.10)

де величина 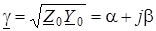зветься коефiцiєнтом поширення.

Для розв'язування однорiдних хвильових рiвнянь (15.10) складемо їх характеристичне рiвняння i визначимо його коренi

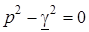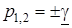; . (15.11)

Загальний розв'язок (15.10), як вiдомо, записується у виглядi

,

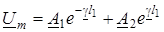де ; 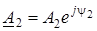- комплекснi сталi iнтегрування.

Цi ж самi сталi визначають розподiл струму в лiнiї:

.

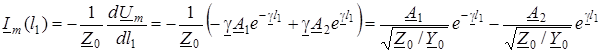Тодi

(15.12)

де 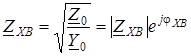зветься хвильовим опором довгої лiнiї.

Перейдемо в (15.12) до миттєвих значень напруги

.

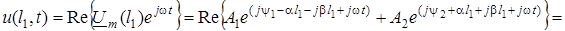
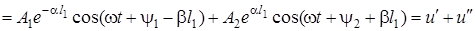З останнього виразу видно, що у будь-якому перерiзi ДЛ у будь-який момент часу миттєве значення напруги (струму) складається з двох доданкiв: u'- пряма (падаюча) хвиля; u" обернена (вiдбита) хвиля. Отже, iснує явище суперпозицiї хвиль. Якщо зафiксувати координату , отримаємо коливання u' з постiйною амплiтудою i початковою фазою; якщо зафiксувати момент t = const, матимемо синусоїдне коливання u' зi згасаючою амплiтудою (рис.15.5а).

Зробимо замiну змiнних у виразi для складової u". Тодi

,

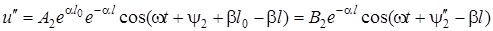де 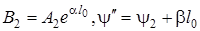- якісь постійні величини.

Графiчно розподiл миттєвих значень напруги падаючої та вiдбитої хвиль вздовж лiнiї показано на рис.15.5 для трьох послiдовних моментiв часу 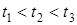. Цi графiки можна розглядати як миттєвi знiмки картини розподiлу напруг падаючої та вiдбитої хвиль у лiнiї. Отже, маємо падаючу хвилю, яка поширюється вiд початку до кiнця лiнiї, та вiдбиту хвилю, яка поширюється вiд кiнця до початку лiнiї.

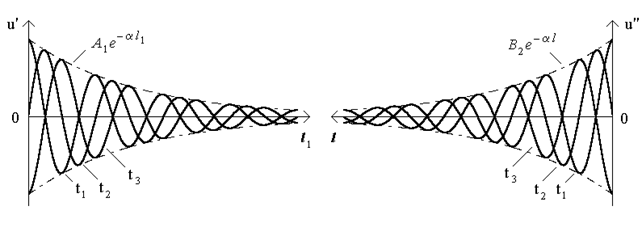
а) б)

Рисунок 15.5

Читайте також:

1. ВТОРИННI ПАРАМЕТРИ ДОВГОЇ ЛIНIЇ
2. Зовнішнє середовище характеризується деякими істотними для організації параметрами.
3. Об'єкти керування, їх математичні моделі. Характеристики об'єктів керування. Одноємнісні об'єкти. Багатоємнісні об'єкти. Об'єкти з розподіленими параметрами.
4. РЕЖИМИ РОБОТИ ДОВГОЇ ЛIНIЇ БЕЗ ВТРАТ

Переглядів: 3610