• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

БАГАТОПОЛЮСНИМИ ЕЛЕМЕНТАМИ

ПЕРЕДАТНI ФУНКЦІЇ СХЕМ З

В попереднiх лекцiях було розглянуто приклади розрахунку передатних функцiй кiл рiзної складностi. Зупинимось на способах визначення передатних функцiй схем з багатополюсними елементами.

13.1 Аналiз схем з багатополюсними елементами

Частина електричного кола, що має понад два виділені затискачi (полюси) зветься багатополюсником (рис.13.1). Аналiз багатополюсника можна проводити як у комплекснiй, так i в операторнiй формi.

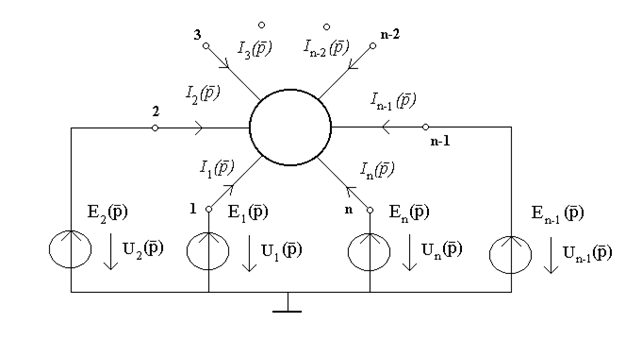
Рисунок 13.1

Вважатимемо струми, якi напрямленi до центру багатополюсника, додатними. Встановимо зв'язок струмiв i е.р.с.. Для iдеальних е.р.с. виконується рiвнiсть . Тодi за теоремою накладання

,

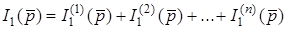або

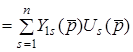. (13.1)

Якщо скласти систему рiвнянь для всiх струмiв , ,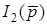... отримаємо основне рiвняння багатополюсника

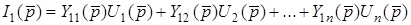
(13.2)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

або в матричнiй формi

, (13.3)

де матриця зветься основним параметром багатополюсника.

Iнакше матриця зветься невизначеною (особливою) матрицею. Розглянемо деякi властивостi особливої матрицi.

Щоб знайти елемент матрицi , замикають всi е.р.с., окрiм 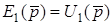, визначають полюсний струм , а потiм - провiднiсть .

Згiдно з першим законом Кiрхгофа .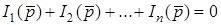

Якщо пiдсумувати рiвняння системи (13.2), отримаємо

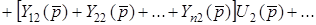
Ця сума дорiвнює нулю при будь-яких напругах. Рiвнiсть нулю виконуватиметься у випадку, коли сума коефiцiєнтiв будь-якого стовпця системи (13.2) дорiвнює нулю. Отже, одержимо першу властивiсть.

1. Сума коефiцiєнтiв будь-якого стовпця матрицi дорiвнює нулю.

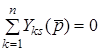, . (13.4)

Можна показати, що сума елементiв всiх рядкiв матрицi також дорiвнюватиме нулю. Нехай до всiх полюсiв багатополюсника пiдключено тiльки джерело 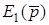(рис.13.2а). Тодi за першим законом Кiрхгофа для єдиного вузла можна записати

.

Оскiльки , то повинна дорiвнювати нулю сума провiдностей. Цей факт обумовлює другу властивiсть.

2. Сума елементiв будь-якого рядка матрицi дорiвнює нулю.

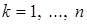, . (13.5)

3. З (13.4) i (13.5) виходить, що визначник матрицi також дорiвнює нулю.

. (13.6)

Якщо виконується умова (13.6), то в системi (13.2) одне з рiвнянь стає зайвим. Воно виключається шляхом заземлювання одного з вузлiв. Отже, одержимо четверту властивiсть.

4. Заземленню n-го вузла вiдповiдає викреслення n-го рядка i n-го стовпця.

Якщо виключити з системи (13.2) n-те рiвняння, матимемо прив'язану (неособливу, скорочену) матрицю 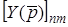. При цьому визначник 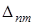не дорiвнюватиме нулю.

5. Об'єднанню вузлiв k та l вiдповiдає пiдсумовування k-го та l-го рядкiв, k-го та l-го стовпцiв. Новим рядку i стовпцю присвоюється iндекс k.

Iнодi замiсть п'ятої властивостi застосовують правила

; (13.7)

; . (13.8)

6. Правило визначення алгебраїчного доповнення

, (13.9)

де a,c - номери рядкiв; b,d номери стовпцiв; сума iндексiв; кiлькiсть iнверсiй, тобто кiлькiсть послiдовних перестановок номерiв рядкiв (стовпцiв) для встановлення iндексiв у порядку збiльшення.

7. Одиночнi iндекси алгебраїчного доповнення, що пiдсумовуються, вказують на номер рядкiв (стовпцiв), якi викреслюються. Перший iндекс у дужках вказує на номер рядка (стовпця), елементи якого переносяться зі знаком, що стоїть за ним, до рядка (стовпця) з номером, який вiдповiдає другому iндексу в дужках.

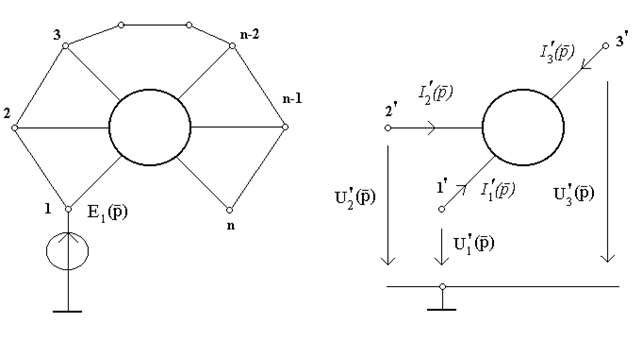
а) б)

Рисунок 13.2

13.2 Узагальнений метод вузлових напруг

У лекцiї 10 розглянуто метод вузлових напруг (МВН) для знаходження операторної функцiї 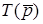. Поширимо цей метод на схеми з багатополюсними елементами. Для спрощення розрахункiв розглянемо триполюсник (рис.13.2б). Для цiєї схеми система (13.2) прийме вигляд

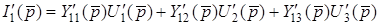
(13.10)

.

Далi розглянемо довiльну схему, яка має двополюснi елементи (рис.13.3а).

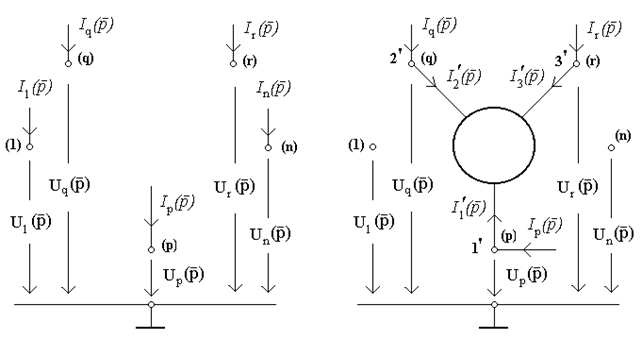а) б)

Рисунок 13.3

Для цiєї схеми запишемо рiвняння, які зв'язують зображення напруг та струмiв .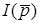

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

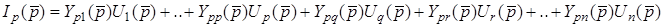
Пiдставимо триполюсник до схеми (рис.13.3б). Тодi для вузла p можна записати

,

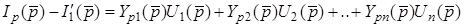звiдки

. (13.11)

Пiдставимо в формулу (13.11) вираз для з (13.10), враховуючи, що ; ; .

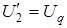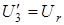. (13.12)

Запишемо невизначену матрицю для схеми без багатополюсника

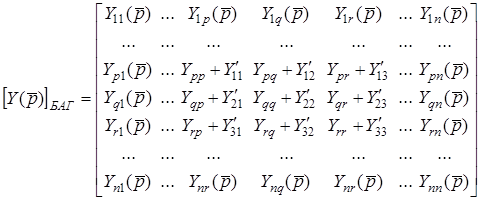. (13.13)

Аналiзуючи рiвняння (13.12) можна зробити висновок, що для переходу до схеми з багатополюсником в матрицю треба внести додатковi доданки. Наприклад, до елемента додається провiднiсть 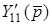, до елемента - провiднiсть 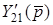i так далi. В пiдсумку одержимо матрицю з урахуванням багатополюсника.

Пiсля визначення матрицi з урахуванням багатополюсника для отримання коефiцiєнта передачi слiд скористатись формулою (10.5). Тодi

.

Отже, сформулюємо правило визначення матрицi з багатополюсником:

1. Скласти матрицю схеми без багатополюсника.

2. Записати матрицю багатополюсника.

3. Перенумерувати рядки i стовпцi у матрицi багатополюсника з урахуванням номерiв тих вузлiв схеми, до яких вiн пiдключається (наприклад, ; ; ).

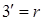4. Пiдсумувати провiдностi у комiрцi зі збіжними номерами.

5. Перевiрити виконання властивостей (13.4), (13.5).

13.3 Розкладання визначника та його алгебраїчних

доповнень за елементами рядка (стовпця)

Аби застосувати формулу (10.5), з'ясуємо, як впливає пiдсумовування додаткових елементiв на властивостi матрицi i всiєї схеми з багатополюсними елементами.

Нехай матриця з урахуванням багатополюсника має вигляд

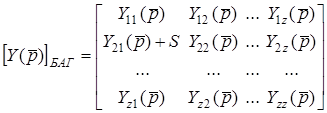. (13.14)

З'ясуємо, як впливає параметр S (тобто додатковi доданки, якi обумовленi впливом багатополюсника) на операторну передатну функцiю схеми.

Наприклад, для визначення за формулою (10.5) коефiцiєнта передачi за напругою , треба розрахувати визначники 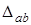i , а для того, щоб розрахувати вузловi напруги за формулою (10.3)

,

необхiдно знати визначник матрицi .

Запишемо визначник матрицi (13.14) згiдно з загальним правилом розкладання за елементами першого стовпця

.

Позначимо 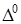- визначник матрицi без урахування багатополюсника. Тодi

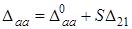; , (13.15)

де a, 2 - номери рядкiв, що викреслюються; a, 1 - номери стовпцiв, що викреслюються.

Читайте також:

1. Аналіз витрат на підприємстві за їх елементами та статтями калькуляції.
2. Взаємодія між елементами інформаційної системи управління.
3. ВЗАЄМОЗВ’ЯЗОК ОПЕРАЦІЙНИХ ВИТРАТ ЗА СТАТТЯМИ ТА ЕЛЕМЕНТАМИ
4. Групування витрат за економічними елементами
5. Догляд за окремими елементами електричних машин
6. Елементами ринку праці виступають : товар, попит, пропозиція та ціна робочої сили.
7. Елементами ринку праці є: товар, який він пропонує, попит, пропозиція та ціна.
8. За економічними елементами і калькуляційними статтями.
9. Зв’язки між його елементами
10. Класифікація витрат за економічними елементами відповідає на питання „скільки чого витрачено?”, а за калькуляційними статтями – „куди понесені витрати?”.
11. КЛАСИФІКАЦІЯ ВИТРАТ ТА ГРУПУВАННЯ ВИТРАТ ЗА ЕКОНОМІЧНИМИ ЕЛЕМЕНТАМИ

Переглядів: 880